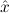 α.
α.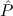 (
(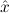 ) →∃
) →∃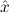 α
α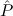 (
(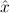 ) (α
) (α τ,
τ,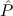 (α)
(α) {
{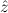 τ ∣ A}))
τ ∣ A}))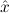 α
α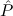 (
(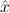 ) → (∀
) → (∀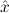 α.
α.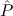 (
(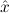 ) →
) →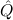 ) →
) →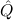
 τ,
τ,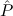 (α)
(α) {
{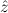 τ ∣ A},
τ ∣ A},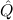
 { ∣ B }))
{ ∣ B }))S:AssumptionVarConst
8.1. Assumption variables. Assumption variables are for proofs what variables are for terms. The main difference, however, is that assumption variables have formulas as types, and that formulas may contain free variables. Therefore we must be careful when substituting terms for variables in assumption variables. Our solution (as in Matthes’ thesis [9]) is to consider an assumption variable as a pair of a (typefree) identifier and a formula, and to take equality of assumption variables to mean that both components are equal. Rather than using symbols as identifiers we prefer to use numbers (i.e. indices). However, sometimes it is useful to provide an optional string as name for display purposes.
We need a constructor, accessors and tests for assumption variables.
| (make-avar formula index name) | constructor | ||||||
| (avar-to-formula avar) | accessor | ||||||
| (avar-to-index avar) | accessor | ||||||
| (avar-to-name avar) | accessor | ||||||
| (avar? x) | test | ||||||
| (avar=? avar1 avar2) | test. |
| (mk-avar formula <index> <name>) |
| (formula-to-new-avar formula) |
An assumption constant appears in a proof, as an axiom, a theorem or a global assumption. Its formula is given as an “uninstantiated formula”, where only type and predicate variables can occur freely; these are considered to be bound in the assumption constant. In the proof the bound type variables are implicitely instantiated by types, and the bound predicate variables by comprehension terms (the arity of a comprehension term is the type-instantiated arity of the corresponding predicate variable). Since we do not have type and predicate quantification in formulas, the assumption constant contains these parts left implicit in the proof: tsubst and pinst (which will become a psubst, once the arities of predicate variables are type-instantiated with tsubst).
So we have assumption constants of the following kinds:
To normalize a proof we will first translate it into a term, then normalize the term and finally translate the normal term back into a proof. To make this work, in case of axioms we pass to the term appropriate formulas: all-formulas for induction, an existential formula for existence introduction, and an existential formula together with a conclusion for existence elimination. During normalization of the term these formulas are passed along. When the normal form is reached, we have to translate back into a proof. Then these formulas are used to reconstruct the axiom in question.
Internally, the formula of an assumption constant is split into an uninstantiated formula where only type and predicate variables can occur freely, and a substitution for at most these type and predicate variables. The formula assumed by the constant is the result of carrying out this substitution in the uninstantiated formula. Note that free variables may again occur in the assumed formula. For example, assumption constants axiomatizing the existential quantifier will internally have the form
(aconst Ex-Intro ∀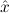 α. α.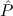 ( (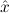 ) →∃ ) →∃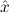 α α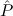 ( (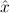 ) (α ) (α τ, τ,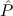 (α) (α) { {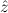 τ ∣ A})) τ ∣ A})) | |||||
(aconst Ex-Elim ∃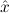 α α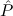 ( (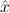 ) → (∀ ) → (∀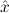 α. α.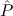 ( (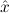 ) → ) →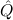 ) → ) →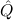 | |||||
(α τ, τ,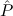 (α) (α) { {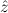 τ ∣ A}, τ ∣ A},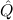  { ∣ B })) { ∣ B })) |
Interface for general assumption constants. To avoid duplication of code it is useful to formulate some procedures generally for arbitrary assumption constants, i.e. for all of the forms listed above.
| (aconst-to-inst-formula aconst) | |||||
| (aconst-to-formula aconst) |
| (aconst? aconst) | |||||
| (aconst=? aconst1 aconst2) | |||||
| (aconst-without-rules? aconst) | |||||
| (aconst-to-string aconst) |
SS:AxiomConst
| =(0,0) | ≈ tt | ||||||
=(0,S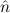 ) ≈ =(S ) ≈ =(S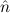 ,0) ,0) | ≈ ff | e(0) | ≈ tt | ||||
=(S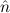 1,S 1,S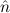 2) 2) | ≈ =(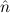 1, 1,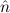 2) 2) | e(S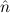 ) ) | ≈ e(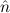 ) ) | ||||
=(bbnat,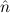 ) ≈ =( ) ≈ =(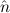 ,bbnat) ,bbnat) | ≈ bb | e(bbnat) | ≈ bb | ||||
=(∞nat,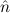 ) ≈ =( ) ≈ =(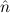 ,∞nat) ,∞nat) | ≈ bb | e(∞nat) | ≈ bb |
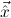 ) → Total(
) → Total(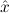 i), the type of
(c
i), the type of
(c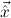 ) need not be a finitary algebra, and hence
) need not be a finitary algebra, and hence 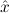 i may have a function
type.
i may have a function
type.
Remark. (E(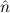 1) →
1) → 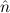 1 =
1 = 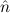 2) → (E(
2) → (E(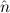 2) →
2) → 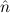 1 =
1 = 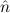 2) →
2) → 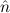 1 ≈
1 ≈ 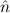 2 is
not valid in our intended model (see Figure 1), since we have two distinct
undefined objects bbnat and ∞nat.
2 is
not valid in our intended model (see Figure 1), since we have two distinct
undefined objects bbnat and ∞nat.
We abbreviate
∀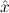 .Totalρ( .Totalρ(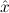 ) → A ) → A | by | ∀xA, | |||||
∃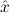 .Totalρ( .Totalρ(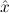 ) ∧ A ) ∧ A | by | ∃xA. |
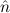 .E(
.E(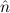 ) →
) →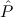 (
(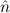 )) →∀n
)) →∀n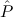 (n) is provable
(since E(n)
(n) is provable
(since E(n) T). Similarly, Ex-ExPartial-nat, i.e. ∃n
T). Similarly, Ex-ExPartial-nat, i.e. ∃n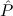 (n) →∃
(n) →∃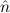 .E(
.E(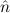 ) ∧
) ∧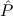 (
(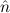 )
is provable.
)
is provable.
Finally we have axioms for the existential quantifier
∀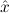 α. α.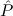 ( (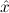 ) →∃ ) →∃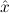 α α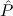 ( (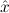 ) ) | Ex-Intro | ||||||
∃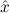 α α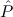 ( (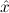 ) → (∀ ) → (∀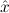 α. α.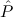 ( (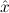 ) → ) →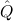 ) → ) →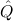 | Ex-Elim |
The assumption constants corresponding to these axioms are
We now spell out what precisely we mean by induction over simultaneous free
algebras 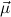 = μ
= μ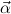
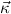 , with goal formulas ∀xjμj
, with goal formulas ∀xjμj 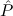 j(xj). For the constructor
type
j(xj). For the constructor
type
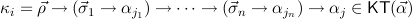
we have the step formula
Di := ∀y1ρ1
,…,ymρm
,ym+1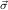 1
→μj1
,…,ym+n 1
→μj1
,…,ym+n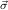 n
→μjn
. n
→μjn
. | ∀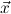 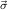 1 1
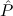 j1(ym+1 j1(ym+1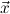 ) → ) →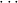 → → | ||
∀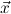 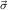 n n
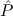 jn(ym+n jn(ym+n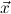 ) → ) → | |||
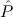 j(constri j(constri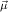 ( (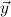 )). )). |
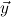 = y1ρ1,…,ymρm,ym+1
= y1ρ1,…,ymρm,ym+1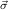 1→μj1,…,ym+n
1→μj1,…,ym+n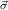 n→μjn are the components of the
object constri
n→μjn are the components of the
object constri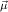 (
(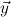 ) of type μj under consideration, and
) of type μj under consideration, and
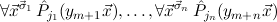
are the hypotheses available when proving the induction step. The induction axiom Indμj then proves the formula
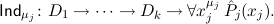
We will often write Indj for Indμj.
An example is
E1 → E2 → E3 → E4 →∀x1tree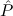 1(x1)
1(x1) | |||||
| with | |||||
E1 := 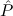 1(Leaf), 1(Leaf), | |||||
E2 := ∀xtlist.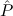 2(x) →
2(x) →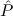 1(Branch(x)), 1(Branch(x)), | |||||
E3 := 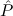 2(Empty), 2(Empty), | |||||
E4 := ∀x1tree,x
2tlist.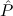 1(x1) →
1(x1) →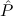 2(x2) → 2(x2) →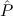 2(Tcons(x1,x2)). 2(Tcons(x1,x2)). | |||||
(aconst Ind E1 → E2 → E3 → E4 →∀x1tree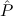 1(x1) 1(x1) | |||||
(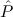 1 1 {x1tree ∣ A1 }, {x1tree ∣ A1 },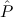 2 2 {x2tlist ∣ A2 })) {x2tlist ∣ A2 })) |
A simplified version (without the recursive calls) of the induction axiom is the following cases axiom.
(aconst Cases E1 → E2 →∀x1tree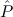 1(x1) ( 1(x1) (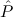 1 1 {x1tree ∣ A1 })) {x1tree ∣ A1 })) | |||||
| with | |||||
E1 := 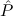 1(Leaf), 1(Leaf), | |||||
E2 := ∀xtlist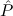 1(Branch(x)).
1(Branch(x)). | |||||
The assumption constants corresponding to these axioms are generated by
| (all-formulas-to-ind-aconst all-formula1 ...) | for Ind | ||||||
| (all-formula-to-cases-aconst all-formula) | for Cases |
For the introduction and elimination axioms Ex-Intro and Ex-Elim for the existential quantifier we provide
| (ex-formula-to-ex-intro-aconst ex-formula) | |||
| (ex-formula-and-concl-to-ex-elim-aconst ex-formula concl) |
To deal with inductively defined predicate constants, we need additional axioms with names “Intro” and “Elim”, which can be generated by
| (number-and-idpredconst-to-intro-aconst i idpc) | |||
| (imp-formulas-to-elim-aconst imp-formula1 ...); |
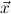 ) → A.
) → A.
SS:Theorems
| (add-theorem string . opt-proof) | or save |
| (theorem-name-to-aconst string) | |||
| (theorem-name-to-proof string) | |||
| (theorem-name-to-inst-proof string) |
| (remove-theorem string1 ...) | |||
| (display-theorems string1 ...) |
Initially we provide the following theorems
Proof of Atom-True. By Ind. In case tt use Eq-Compat with tt ≈ =(tt,tt) to infer atom(=(tt,tt)) (i.e. tt = tt) from atom(tt). In case ff use Eq-Compat with ff ≈ =(ff,tt) to infer atom(=(ff,tt)) (i.e. ff = tt) from atom(ff). _
Proof of Atom-False. Use Ind, and Truth-Axiom in both cases. – Notice
that the more general (atom(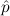 ) → F) →
) → F) →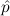 = ff does not hold with bb for
= ff does not hold with bb for 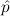 ,
since =(bb,ff) ≈ bb. _
,
since =(bb,ff) ≈ bb. _
Proof of Efq-Atom. Again by Ind. In case tt use Truth-Axiom, and the case ff is obvious. _
Proof of Stab-Atom. By Ind. In case tt use Truth-Axiom, and the case ff is obvious. _
Remark. Notice that from Efq-Atom one easily obtains F → A for every
formula A all whose strictly positions occurrences of prime formulas are of
the form atom(r), by induction on A. For all other formulas we shall make use
of the global assumption Efq: F → 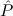 (cf. Section 8.4). Similarly, Notice
that from Stab-Atom one again obtains ((A → F) → F) → A for every
formula A all whose strictly positions occurrences of prime formulas are of
the form atom(r), by induction on A. For all other formulas we shall make
use of the global assumption Stab: ((
(cf. Section 8.4). Similarly, Notice
that from Stab-Atom one again obtains ((A → F) → F) → A for every
formula A all whose strictly positions occurrences of prime formulas are of
the form atom(r), by induction on A. For all other formulas we shall make
use of the global assumption Stab: ((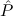 → F) → F) →
→ F) → F) →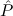 (cf. Section 8.4).
(cf. Section 8.4).
Proof of =-Refl-nat. Use Ind, and Truth-Axiom in both cases. – Notice
that  =
= 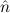 does not hold, since =(bb,bb) ≈ bb. _
does not hold, since =(bb,bb) ≈ bb. _
Here are some other examples of theorems; we give the internal representation
as assumption constants, which show how the assumed formula is split into an
uninstantiated formula and a substitution, in this case a type substitution α ρ,
an object substitution fα→nat
ρ,
an object substitution fα→nat gρ→nat and a predicate variable substitution
gρ→nat and a predicate variable substitution
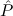 (α)
(α) {
{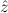 ρ ∣ A}.
ρ ∣ A}.
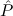 , and the second that we quantify over just
one variable x. Both theorems can easily be generalized to more such
parameters.
, and the second that we quantify over just
one variable x. Both theorems can easily be generalized to more such
parameters.
When dealing with classical logic it will be useful to have
(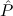 → →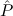 1) → (( 1) → ((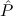 →⊥) → →⊥) →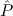 1) → 1) →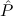 1 1 | Cases-Log |
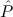 1; hence we
cannot extract a term from it.
1; hence we
cannot extract a term from it.
The assumption constants corresponding to these theorems are generated by
| (theorem-name-to-aconst name) |
SS:GlobalAss
| (add-global-assumption name formula) (abbreviated aga) | |||
| (remove-global-assumption string1 ...) | |||
| (display-global-assumptions string1 ...) |
We initially supply global assumptions for ex-falso-quodlibet and stability, both in logical and arithmetical form (for our two forms of falsity).
⊥→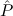 | Efq-Log | ||||||
((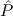 →⊥) →⊥) → →⊥) →⊥) →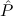 | Stab-Log | ||||||
F →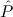 | Efq | ||||||
((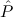 → F) → F) → → F) → F) →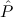 | Stab |
| (global-assumption-name-to-aconst name) |