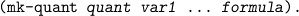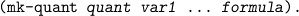7. Formulas and comprehension terms
A prime formula can have the form
- (atom r) with a term r of type boole,
- (predicate a r1 ... rn) with a predicate variable or constant a
and terms r1 ...rn.
Formulas are built from prime formulas by
- implication (imp formula1 formula2)
- conjunction (and formula1 formula2)
- tensor (tensor formula1 formula2)
- all quantification (all x formula)
- existential quantification (ex x formula)
- all quantification (allnc x formula) without computational
content
- existential quantification (exnc x formula) without
computational content
Moreover we have classical existential quantification in an arithmetical and a logical
form:
| (exca (x1...) formula) | | arithmetical version | | | |
|
| (excl (x1 ...) formula) | | logical version. | | | | |
Here we allow that the quantified variable is formed without ˆ, i.e. ranges over
total objects only.
Formulas can be unfolded in the sense that the all classical existential
quantifiers are replaced according to their definiton. Inversely a formula can be
folded in the sense that classical existential quantifiers are introduced wherever
possible.
Comprehension terms have the form (cterm vars formula). Note that
formula may contain further free variables.
Tests:
| (atom-form? formula) | |
|
| (predicate-form? formula) | |
|
| (prime-form? formula) | |
|
| (imp-form? formula) | |
|
| (and-form? formula) | |
|
| (tensor-form? formula) | |
|
| (all-form? formula) | |
|
| (ex-form? formula) | |
|
| (allnc-form? formula) | |
|
| (exnc-form? formula) | |
|
| (exca-form? formula) | |
|
| (excl-form? formula) | | |
and also
| (quant-prime-form? formula) | |
|
| (quant-free? formula). | | |
We need constructors and accessors for prime formulas
| (make-atomic-formula boolean-term) | | | |
|
| (make-predicate-formula predicate term1 ...) | | | |
|
| atom-form-to-kernel | | | |
|
| predicate-form-to-predicate | | | |
|
| predicate-form-to-args. | | | | |
We also have constructors for special atomic formulas
| (make-eq term1 term2) | | constructor for equalities | | | |
|
| (make-= term1 term2) | | constructor for equalities on finalgs | | | |
|
| (make-total term) | | constructor for totalities | | | |
|
| (make-e term) | | constructor for existence on finalgs | | | |
|
| truth | | | |
|
| falsity | | | |
|
| falsity-log. | | | | |
We need constructors and accessors for implications
| (make-imp premise conclusion) | | constructor | | | |
|
| (imp-form-to-premise imp-formula) | | accessor | | | |
|
| (imp-form-to-conclusion imp-formula) | | accessor, | | | | |
conjunctions
| (make-and formula1 formula2) | | constructor | | | |
|
| (and-form-to-left and-formula) | | accessor | | | |
|
| (and-form-to-right and-formula) | | accessor, | | | | |
tensors
| (make-tensor formula1 formula2) | | constructor | | | |
|
| (tensor-form-to-left tensor-formula) | | accessor | | | |
|
| (tensor-form-to-right tensor-formula) | | accessor, | | | | |
universally quantified formulas
| (make-all var formula) | | constructor | | | |
|
| (all-form-to-var all-formula) | | accessor | | | |
|
| (all-form-to-kernel all-formula) | | accessor, | | | | |
existentially quantified formulas
| (make-ex var formula) | | constructor | | | |
|
| (ex-form-to-var ex-formula) | | accessor | | | |
|
| (ex-form-to-kernel ex-formula) | | accessor, | | | | |
universally quantified formulas without computational content
| (make-allnc var formula) | | constructor | | | |
|
| (allnc-form-to-var allnc-formula) | | accessor | | | |
|
| (allnc-form-to-kernel allnc-formula) | | accessor, | | | | |
existentially quantified formulas without computational content
| (make-exnc var formula) | | constructor | | | |
|
| (exnc-form-to-var exnc-formula) | | accessor | | | |
|
| (exnc-form-to-kernel exnc-formula) | | accessor, | | | | |
existentially quantified formulas in the sense of classical arithmetic
| (make-exca var formula) | | constructor | | | |
|
| (exca-form-to-var exca-formula) | | accessor | | | |
|
| (exca-form-to-kernel exca-formula) | | accessor, | | | | |
existentially quantified formulas in the sense of classical logic
| (make-excl var formula) | | constructor | | | |
|
| (excl-form-to-var excl-formula) | | accessor | | | |
|
| (excl-form-to-kernel excl-formula) | | accessor. | | | | |
For convenience we also have as generalized constructors
| (mk-imp formula formula1 ...) | | implication | | | |
|
| (mk-neg formula1 ...) | | negation | | | |
|
| (mk-neg-log formula1 ...) | | logical negation | | | |
|
| (mk-and formula formula1 ...) | | conjunction | | | |
|
| (mk-tensor formula formula1 ...) | | tensor | | | |
|
| (mk-all var1 ... formula) | | all-formula | | | |
|
| (mk-ex var1 ... formula) | | ex-formula | | | |
|
| (mk-allnc var1 ... formula) | | allnc-formula | | | |
|
| (mk-exnc var1 ... formula) | | exnc-formula | | | |
|
| (mk-exca var1 ... formula) | | classical ex-formula (arithmetical) | | | |
|
| (mk-excl var1 ... formula) | | classical ex-formula (logical) | | | | |
and as generalized accessors
| (imp-form-to-premises-and-final-conclusion formula) | | | |
|
| (tensor-form-to-parts formula) | | | |
|
| (all-form-to-vars-and-final-kernel formula) | | | |
|
| (ex-form-to-vars-and-final-kernel formula) | | | | |
and similarly for exca-forms and excl-forms. Occasionally it is convenient to
have
| (imp-form-to-premises formula <n>) | | all (first n) premises | | | |
|
| (imp-form-to-final-conclusion formula <n>) | | | | |
where the latter computes the final conclusion (conclusion after removing the
first n premises) of the formula.
It is also useful to have some general procedures working for arbitrary
quantified formulas. We provide
| (make-quant-formula quant var1 ... kernel) | | constructor | | | |
|
| (quant-form-to-quant quant-form) | | accessor | | | |
|
| (quant-form-to-vars quant-form) | | accessor | | | |
|
| (quant-form-to-kernel quant-form) | | accessor | | | |
|
| (quant-form? x) | | test. | | | | |
and for convenience also
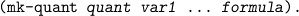
To fold and unfold formulas we have
| (fold-formula formula) | |
|
| (unfold-formula formula). | | |
To test equality of formulas up to normalization and α-equality we use
| (classical-formula=? formula1 formula2) | |
|
| (formula=? formula1 formula2), | | |
where in the first procedure we unfold before comparing.
Morever we need
| (formula-to-free formula), | |
|
| (nbe-formula-to-type formula), | |
|
| (formula-to-prime-subformulas formula), | | |
Constructors, accessors and a test for comprehension terms are
| (make-cterm var1 ... formula) | | constructor | | | |
|
| (cterm-to-vars cterm) | | accessor | | | |
|
| (cterm-to-formula cterm) | | accessor | | | |
|
| (cterm? x) | | test. | | | | |
Moreover we need
| (cterm-to-free cterm) | |
|
| (cterm=? x) | |
|
| (classical-cterm=? x) | |
|
| (fold-cterm cterm) | |
|
| (unfold-cterm cterm). | | |
Normalization of formulas is done with
| (normalize-formula formula) | | normalization, | | | | |
abbreviated nf.
To check equality of formulas we use
| (classical-formula=? formula1 formula2) | | | |
|
| (formula=? formula1 formula2) | | | | |
where the former unfolds the classical existential quantifiers and normalizes all
subterms in its formulas.
Display functions for formulas and comprehension terms are
| (formula-to-string formula) | | | |
|
| (cterm-to-string cterm). | | | | |
The former is abbreviated nf.
We can define simultaneous substitution for type, object and predicate
variables in a formula, via tsubst, subst and psubst. It is assumed that subst
only affects those variables whose type is not changed by tsubst, and that
psubst only affects those predicate variables whose arity is not changed by
tsubst.
In the quantifier case of the recursive definition, the abstracted variable may
need to be renamed. However, its type can be affected by tsubst. Then the
renaming cannot be made part of subst, because then the condition
above would be violated. Therefore we carry along a procedure rename
renaming variables, which remembers the renaming of variables done so
far.
We will also need formula substitution to compute the formula of an
assumption constant. However, there (type and) predicate variables are
(implicitely) considered to be bound. Therefore, we also have to carry along a
procedure prename renaming predicate variables, which remembers the renaming
of predicate variables done so far.
| (formula-substitute formula topsubst) | | | |
|
| (formula-subst formula arg val) | | | |
|
| (cterm-substitute cterm topsubst) | | | |
|
| (cterm-subst cterm arg val) | | | | |
Display functions for predicate substitutions are
| (display-p-substitution psubst) | |
|
| (p-substitution-to-string psubst) | | |