6. Terms and objects
Terms are built from (typed) variables and constants by abstraction,
application, pairing, formation of left and right components (i.e. projections) and
the if-construct.
The if-construct distinguishes cases according to the outer constructor form;
the simplest example (for the type boole) is if-then-else. Here we do
not want to evaluate all arguments right away, but rather evaluate the
test argument first and depending on the result evaluate at most one
of the other arguments. This phenomenon is well known in functional
languages; e.g. in Scheme the if-construct is called a special form as
opposed to an operator. In accordance with this terminology we also call
our if-construct a special form. It will be given a special treatment in
nbe-term-to-object.
Usually it will be the case that every closed term of an sfa ground type reduces
via the computation rules to a constructor term, i.e. a closed term built from
constructors only. However, we do not require this.
We have constructors, accessors and tests for variables
| (make-term-in-var-form var) | | constructor | | | |
|
| (term-in-var-form-to-var term) | | accessor, | | | |
|
| (term-in-var-form? term) | | test, | | | | |
for constants
| (make-term-in-const-form const) | | constructor | | | |
|
| (term-in-const-form-to-const term) | | accessor | | | |
|
| (term-in-const-form? term) | | test, | | | | |
for abstractions
| (make-term-in-abst-form var term) | | constructor | | | |
|
| (term-in-abst-form-to-var term) | | accessor | | | |
|
| (term-in-abst-form-to-kernel term) | | accessor | | | |
|
| (term-in-abst-form? term) | | test, | | | | |
for applications
| (make-term-in-app-form term1 term2) | | constructor | | | |
|
| (term-in-app-form-to-op term) | | accessor | | | |
|
| (term-in-app-form-to-arg term) | | accessor | | | |
|
| (term-in-app-form? term) | | test, | | | | |
for pairs
| (make-term-in-pair-form term1 term2) | | constructor | | | |
|
| (term-in-pair-form-to-left term) | | accessor | | | |
|
| (term-in-pair-form-to-right term) | | accessor | | | |
|
| (term-in-pair-form? term) | | test, | | | | |
for the left and right component of a pair
| (make-term-in-lcomp-form term) | | constructor | | | |
|
| (make-term-in-rcomp-form term) | | constructor | | | |
|
| (term-in-lcomp-form-to-kernel term) | | accessor | | | |
|
| (term-in-rcomp-form-to-kernel term) | | accessor | | | |
|
| (term-in-lcomp-form? term) | | test | | | |
|
| (term-in-rcomp-form? term) | | test | | | | |
and for if-constructs
| (make-term-in-if-form test alts . rest) | | constructor | | | |
|
| (term-in-if-form-to-test term) | | accessor | | | |
|
| (term-in-if-form-to-alts term) | | accessor | | | |
|
| (term-in-if-form-to-rest term) | | accessor | | | |
|
| (term-in-if-form? term) | | test. | | | | |
where in make-term-in-if-form, rest is either empty or an all-formula.
It is convenient to have more general application constructors and accessors
available, where application takes arbitrary many arguments and works for
ordinary application as well as for component formation.
| (mk-term-in-app-form term term1 ...) | | constructor | | | |
|
| (term-in-app-form-to-final-op term) | | accessor | | | |
|
| (term-in-app-form-to-args term) | | accessor, | | | | |
Also for abstraction it is convenient to have a more general constructor taking
arbitrary many variables to be abstracted one after the other
| (mk-term-in-abst-form var1 ... term). | | | | |
We also allow vector notation for recursion (cf. Joachimski and Matthes
[8]).
Moreover we need
| (term? x) | | | |
|
| (term=? term1 term2) | | | |
|
| (terms=? terms1 terms2) | | | |
|
| (term-to-type term) | | | |
|
| (term-to-free term) | | | |
|
| (term-to-bound term) | | | |
|
| (term-to-t-deg term) | | | |
|
| (synt-total? term) | | | |
|
| (term-to-string term). | | | | |
6.1. Normalization.
We need an operation which transforms a term into its normal form w.r.t. the
given computation and rewrite rules. Here we base our treatment on
normalization by evaluation introduced in [5], and extended to arbitrary
computation and rewrite rules in [4].
For normalization by evaluation we need semantical objects. For an arbitrary
ground type every term family of that type is an object. For an sfa ground
type, in addition the constructors have semantical counterparts. The
freeness of the constructors is expressed by requiring that their ranges are
disjoint and that they are injective. Moreover, we view the free algebra as a
domain and require that its bottom element is not in the range of the
constructors. Hence the constructors are total and non-strict. Then by
applying nbe-reflect followed by nbe-reify we can normalize every term,
where normalization refers to the computation as well as the rewrite
rules.
An object consists of a semantical value and a type.
| (nbe-make-object type value) | | constructor | | | |
|
| (nbe-object-to-type object) | | accessor | | | |
|
| (nbe-object-to-value object) | | accessor | | | |
|
| (nbe-object? x) | | test. | | | | |
To work with objects, we need
| (nbe-object-apply function-obj arg-obj) | | | | |
Again it is convenient to have a more general application operation available,
which takes arbitrary many arguments and works for ordinary application as well
as for component formation. We also need an operation composing two unary
function objects.
| (nbe-object-app function-obj arg-obj1 ...) | | | |
|
| (nbe-object-compose function-obj1 function-obj2) | | | | |
For ground type values we need constructors, accessors and tests. To make
constructors “self-evaluating”, a constructor value has the form
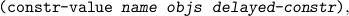
where delayed-constr is a procedure of zero arguments which evaluates to this
very same constructor. This is necessary to avoid having a cycle (for nullary
constructors, and only for those).
| (nbe-make-constr-value name objs) | | constructor | | | |
|
| (nbe-constr-value-to-name value) | | accessor | | | |
|
| (nbe-constr-value-to-args value) | | accessor | | | |
|
| (nbe-constr-value-to-constr value) | | accessor | | | |
|
| (nbe-constr-value? value) | | test | | | |
|
| (nbe-fam-value? value) | | test. | | | | |
The essential function which “animates” the program constants according to the
given computation and rewrite rules is
| (nbe-pconst-and-tsubst-and-rules-to-object | |
|
| pconst tsubst comprules rewrules) | | |
Using it we can the define an evaluation function, which assigns to a term and an
environment a semantical object:
| (nbe-term-to-object term bindings) | | evaluation. | | | | |
Here bindings is an association list assigning objects of the same type to
variables. In case a variable is not assigned anything in bindings, by default we
assign the constant term family of this variable, which always is an object of the
correct type.
The interpretation of the program constants requires some auxiliary functions
(cf. [4]):
| (nbe-constructor-pattern? term) | | test | | | |
|
| (nbe-inst? constr-pattern obj) | | test | | | |
|
| (nbe-genargs constr-pattern obj) | | generalized arguments | | | |
|
| (nbe-extract termfam) | | extracts a term from a family | | | |
|
| (nbe-match pattern term) | | | | |
Then we can define
| (nbe-reify object) | | reification | | | |
|
| (nbe-reflect term) | | reflection | | | | |
and by means of these
| (nbe-normalize-term term) | | normalization, | | | | |
abbreviated nt.
The if-form needs a special treatment. In particular, for a full normalization
of terms (including permutative conversions), we define a preprocessing step that
η expands the alternatives of all if-terms. The result contains if-terms with
ground type alternatives only.
6.2. Substitution.
Recall the generalities on substitutions in Section 2.1.
We define simultaneous substitution for type and object variables in a term,
via tsubst and subst. It is assumed that subst only affects those vars whose
type is not changed by tsubst.
In the abstraction case of the recursive definition, the abstracted variable may
need to be renamed. However, its type can be affected by tsubst. Then the
renaming cannot be made part of subst, because the condition above would be
violated. Therefore we carry along a procedure renaming variables, which
remembers the renaming of variables done so far.
| (term-substitute term tosubst) | | | |
|
| (term-subst term arg val) | | | |
|
| (compose-o-substitutions subst1 subst2) | | | | |
The o in compose-o-substitutions indicates that we substitute for object
variables. However, since this is the most common form of substitution, we also
write compose-substitutions instead.
Display functions for substitutions are
| (display-substitution subst) | |
|
| (substitution-to-string subst) | | |