[next] [prev] [prev-tail] [tail] [up]

5. Predicate variables and constants

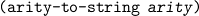
S:Psyms

5.1. Predicate variables.

SS:PredVars

A predicate variable of arity ρ1,…,ρn is a placeholder for a formula A with distinguished (different) variables x1,…,xn of types ρ1,…,ρn. Such an entity is called a comprehension term, written {x1,…,xn ∣ A}.

Predicate variable names are provided in the form of an association list, which assigns to the names their arities. By default we have the predicate variable bot of arity (arity), called (logical) falsity. It is viewed as a predicate variable rather than a predicate constant, since (when translating a classical proof into a constructive one) we want to substitute for bot.

Often we will argue about Harrop formulas only, i.e. formulas without computational content. For convenience we use a special sort of predicate variables intended to range over comprehension terms with Harrop formulas only. For example, P0,P1,P2,…,Q0,… range over comprehension terms with Harrop formulas, and Pˆ0,Pˆ1,Pˆ2,… are general predicate variables. We say that Harrop degree for the former is 1, and for the latter 0.

We need constructors and accessors for arities

(make-arity type1 ...)
(arity-to-types arity)
To display an arity we have
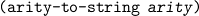
(arity -to-string arity )

We can test whether a string is a name for a predicate variable, and if so compute its associated arity:

(pvar-name? string)
(pvar-name-to-arity pvar-name)

To add and remove names for predicate variables of a given arity (e.g. Q for predicate variables of arity nat), we use

(add-pvar-name name1 ... arity)
(remove-pvar-name name1 ...)

We need a constructor, accessors and tests for predicate variables.

(make-pvar arity index h-deg name) constructor
(pvar-to-arity pvar) accessor
(pvar-to-index pvar) accessor
(pvar-to-h-deg pvar) accessor
(pvar-to-name pvar) accessor
(pvar? x)
(equal-pvars? pvar1 pvar2)

For convenience we have the function

(mk-pvar arity <index> <h-deg> <name>)
The arity is a required argument; the remaining arguments are optional. The default for index is -1, for h-deg is 1 (i.e. Harrop-formula) and for name it is given by (default-pvar-name arity).

It is guaranteed that parsing a displayed predicate variable reproduces the predicate variable; the converse need not be the case (we may want to convert it into some canonical form).

5.2. Predicate constants.

SS:PredConsts

We also allow predicate constants. The general reason for having them is that we need predicates to be axiomatized, e.g. Equal and Total (which are not placeholders for formulas). Prime formulas built from predicate constants do not give rise to extracted terms, and cannot be substituted for.

Notice that a predicate constant does not change its name under a type substitution; this is in contrast to predicate (and other) variables. Notice also that the parser can infer from the arguments the types ρ1…ρn to be substituted for the type variables in the uninstantiated arity of P.

To add and remove names for predicate constants of a given arity, we use

(add-predconst-name name1 ... arity)
(remove-predconst-name name1 ...)
We need a constructor, accessors and tests for predicate constants.
(make-predconst uninst-arity tsubst index name) constructor
(predconst-to-uninst-arity predconst) accessor
(predconst-to-tsubst predconst) accessor
(predconst-to-index predconst) accessor
(predconst-to-name predconst) accessor
(predconst? x)
Moreover we need
(predconst-name? name)
(predconst-name-to-arity predconst-name).
(predconst-to-string predconst).

5.3. Inductively defined predicate constants.

SS:IDPredConsts

As we have seen, type variables allow for a general treatment of inductively generated types μ⃗α⃗κ. Similarly, we can use predicate variables to inductively generate predicates μ ⃗ X⃗ K.

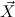
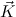More precisely, we allow the formation of inductively generated predicates μ⃗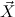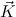X⃗K, where ⃗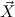X = (Xj)j=1,…,N is a list of distinct predicate variables, and 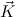K⃗ = (Ki)i=1,…,k is a list of constructor formulas (or “clauses”) containing X1,…,XN in strictly positive positions only.

To introduce inductively defined predicates we use

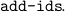
add-ids.

An example is

(add-ids (list (list "Ev" (make-arity (py "nat")) "algEv")  
               (list "Od" (make-arity (py "nat")) "algOd"))  
         ’("Ev 0" "InitEv")  
         ’("allnc n.Od n -> Ev(n+1)" "GenEv")  
         ’("Od 1" "InitOd")  
         ’("allnc n.Ev n -> Od(n+1)" "GenOd"))

This simultaneously introduces the two inductively defined predicate constants Ev and Od, by the clauses given. The presence of an algebra name after the arity (here algEv and algOd) indicates that this inductively defined predicate constant is to have computational content. Then all clauses with this constant in the conclusion must provide a constructor name (here InitEv, GenEv, InitOd, GenOd). If the constant is to have no computational content, then all its clauses must be invariant (under realizability, a.k.a. “negative”).

Here are some further examples of inductively defined predicates:

(add-ids  
  (list (list "Even" (make-arity (py "nat")) "algEven"))  
  ’("Even 0" "InitEven")  
  ’("allnc n.Even n -> Even(n+2)" "GenEven"))  
 
(add-ids  
  (list (list "Acc" (make-arity (py "nat")) "algAcc"))  
  ’("allnc n.(all m.m<n -> Acc m) -> Acc n" "GenAccSup"))  
 
(add-ids (list (list "OrID" (make-arity) "algOrID"))  
         ’("Pˆ1 -> OrID" "InlOrID")  
         ’("Pˆ2 -> OrID" "InrOrID"))  
 
(add-ids  
  (list (list "EqID" (make-arity (py "alpha") (py "alpha"))  
              "algEqID"))  
  ’("allnc xˆ EqID xˆ xˆ" "GenEqID"))  
 
(add-ids (list (list "ExID" (make-arity) "algExID"))  
         ’("allnc xˆ.Qˆ xˆ -> ExID" "GenExID"))  
 
(add-ids  
  (list (list "FalsityID" (make-arity) "algFalsityID")))

[next] [prev] [prev-tail] [front] [up]