 ρ. This is done for clarity (and brevity, e.g. for large ρ in the
example above), since one should think of the type of a constant in this
way.
ρ. This is done for clarity (and brevity, e.g. for large ρ in the
example above), since one should think of the type of a constant in this
way.
Pconst
The latter are built into the system: recursion operators for arbitrary algebras,
equality and existence operators for finitary algebras, and existence elimination.
They are typed in parametrized form, with the actual type (or formula) given
by a type (or type and formula) substitution that is also part of the
constant. For instance, equality is typed by α → α → boole and a type
substitution α ρ. This is done for clarity (and brevity, e.g. for large ρ in the
example above), since one should think of the type of a constant in this
way.
ρ. This is done for clarity (and brevity, e.g. for large ρ in the
example above), since one should think of the type of a constant in this
way.
For constructors and for constants with fixed rules, by efficiency reasons we want to keep the object denoted by the constant (as needed for normalization by evaluation) as part of it. It depends on the type of the constant, hence must be updated in a given proof whenever the type changes by a type substitution.
4.1. Rewrite and computation rules for program constants.
SS:RewCompRules
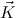
 N are given, where FV(N) ⊆ FV(
N are given, where FV(N) ⊆ FV(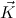 ) and c
) and c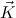 , N have the
same type (not necessarily a ground type). Moreover, for any two rules c
, N have the
same type (not necessarily a ground type). Moreover, for any two rules c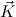
 N
and c
N
and c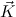 ′
′ N′ we require that
N′ we require that 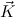 and
and 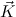 ′ are of the same length, called the arity
of c. The rules are divided into computation rules and proper rewrite rules. They
must satisfy the requirements listed in [4]. The idea is that a computation
rule can be understood as a description of a computation in a suitable
semantical model, provided the syntactic constructors correspond to
semantic ones in the model, whereas the other rules describe syntactic
transformations.
′ are of the same length, called the arity
of c. The rules are divided into computation rules and proper rewrite rules. They
must satisfy the requirements listed in [4]. The idea is that a computation
rule can be understood as a description of a computation in a suitable
semantical model, provided the syntactic constructors correspond to
semantic ones in the model, whereas the other rules describe syntactic
transformations.
There a more general approach was used: one may enter into components of
products. Then instead of one arity one needs several “type informations” 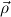 → σ
with
→ σ
with 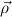 a list of types, 0’s and 1’s indicating the left or right part of a product
type. For example, if c is of type τ → (τ → τ → τ) × (τ → τ), then the rules
cy0xx
a list of types, 0’s and 1’s indicating the left or right part of a product
type. For example, if c is of type τ → (τ → τ → τ) × (τ → τ), then the rules
cy0xx a and cy1
a and cy1 b are admitted, and c comes with the type informations
(τ,0,τ,τ → τ) → τ and (τ,1) → (τ → τ). – However, for simplicity we only deal
with a single arity here.
b are admitted, and c comes with the type informations
(τ,0,τ,τ → τ) → τ and (τ,1) → (τ → τ). – However, for simplicity we only deal
with a single arity here.
Given a set of rewrite rules, we want to treat some rules - which we call computation rules - in a different, more efficient way. The idea is that a computation rule can be understood as a description of a computation in a suitable semantical model, provided the syntactic constructors correspond to semantic ones in the model, whereas the other rules describe syntactic transformations.
In order to define what we mean by computation rules, we need the notion of a constructor pattern. These are special terms defined inductively as follows.
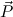 is of ground type, then c
is of ground type, then c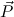 is a constructor pattern.
is a constructor pattern.From the given set of rewrite rules we choose a subset Comp with the following properties.
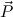
 Q ∈ Comp, then P1,…,Pn are constructor patterns or
projection markers.
Q ∈ Comp, then P1,…,Pn are constructor patterns or
projection markers.
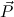
 Q ∈ Comp, then every variable
in c
Q ∈ Comp, then every variable
in c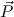 occurs only once in c
occurs only once in c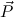 .
.
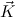
 M and
c
M and
c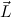
 N in Comp the left hand sides c
N in Comp the left hand sides c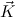 and c
and c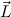 are non-unifiable.
are non-unifiable.We write c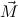
 compQ to indicate that the rule is in Comp. All other rules will be
called (proper) rewrite rules, written c
compQ to indicate that the rule is in Comp. All other rules will be
called (proper) rewrite rules, written c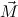
 rewK.
rewK.
In our reduction strategy computation rules will always be applied first, and
since they are non-overlapping, this part of the reduction is unique. However,
since we allowed almost arbitrary rewrite rules, it may happen that in case no
computation rule applies a term may be rewritten by different rules 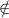 Comp. In
order to obtain a deterministic procedure we then select the first applicable
rewrite rule (This is a slight simplification of [4], where special functions selc were
used for this purpose).
Comp. In
order to obtain a deterministic procedure we then select the first applicable
rewrite rule (This is a slight simplification of [4], where special functions selc were
used for this purpose).
4.2. Recursion over simultaneous free algebras.
SS:RecSFA
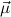 = μ
= μ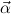
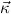 corresponds to two
sorts of constants. With the constructors constri
corresponds to two
sorts of constants. With the constructors constri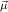 : κi[
: κi[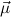 ] we can construct
elements of a type μj, and with the recursion operators ℛμj
] we can construct
elements of a type μj, and with the recursion operators ℛμj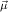 ,
,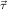 we can
construct mappings from μj to τj by recursion on the structure of
we can
construct mappings from μj to τj by recursion on the structure of 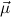 . So in
(Rec arrow-types), arrow-types is a list μ1 → τ1,…,μk → τk. Here
μ1,…,μk are the algebras defined simultaneously and τ1,…,τk are the result
types.
. So in
(Rec arrow-types), arrow-types is a list μ1 → τ1,…,μk → τk. Here
μ1,…,μk are the algebras defined simultaneously and τ1,…,τk are the result
types.
For convenience in our later treatment of proofs (when we want to normalize a proof by (1) translating it into a term, (2) normalizing this term and (3) translating the normal term back into a proof), we also allow all-formulas ∀x1μ1A1,…,∀xkμkAk instead of arrow-types: they are treated as μ1 → τ(A1), ..., μk → τ(Ak) with τ(Aj) the type of Aj.
Recall the definition of types and constructor types in Section 2, and the
examples given there. In order to define the type of the recursion operators
w.r.t. 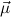 = μ
= μ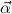
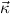 and result types
and result types 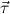 , we first define for
, we first define for
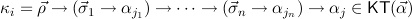
the step type
δi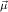 , ,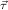 := := 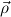 → → | (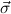 1 → μj1) →
1 → μj1) → → ( → (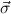 n → μjn) → n → μjn) → | ||
(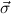 1 → τj1) → 1 → τj1) →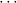 → ( → (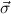 n → τjn) → τj. n → τjn) → τj. |
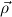 ,(
,(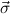 1 → μj1),…,(
1 → μj1),…,(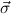 n → μjn) correspond to the components of the object of
type μj under consideration, and (
n → μjn) correspond to the components of the object of
type μj under consideration, and (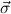 1 → τj1),…,(
1 → τj1),…,(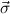 n → τjn) to the previously
defined values. The recursion operator ℛμj
n → τjn) to the previously
defined values. The recursion operator ℛμj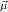 ,
,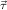 has type
has type
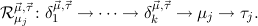
We will often write ℛj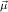 ,
,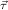 for ℛμj
for ℛμj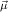 ,
,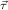 , and omit the upper indices
, and omit the upper indices 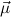 ,
,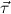 when
they are clear from the context. In case of a non-simultaneous free algebra, i.e. of
type μα (κ), for ℛμμ,τ we normally write ℛμτ.
when
they are clear from the context. In case of a non-simultaneous free algebra, i.e. of
type μα (κ), for ℛμμ,τ we normally write ℛμτ.
A simple example for simultaneous free algebras is
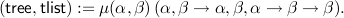
The constructors are
| Leaftree := constr 1(tree,tlist), | |||
| Branchtlist→tree := constr 2(tree,tlist), | |||
| Emptytlist := constr 3(tree,tlist), | |||
| Tconstree→tlist→tlist := constr 4(tree,tlist). |
| (const Rec δ1 → δ2 → δ3 → δ4 → tree → α1 | |||||
(α1 τ1,α2 τ1,α2 τ2)) τ2)) | |||||
| with | |||||
| δ1 := α1, | |||||
| δ2 := tlist → α2 → α1, | |||||
| δ3 := α2, | |||||
| δ4 := tree → tlist → α1 → α2 → α2. | |||||
For the external representation (i.e. display) we use the shorter notation
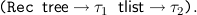
As already mentioned, it is also possible that the object constant Rec comes with formulas instead of types, as the assumption constant Ind below. This is due to our desire not to duplicate code when normalizing proofs, but rather translate the proof into a term first, normalize the term and then translate back into a proof. For the last step we must have the original formulas of the induction operator available.
To see a concrete example, let us recursively define addition +: tree → tree → tree and ⊕: tlist → tree → tlist. The recursion equations to be satisfied are
| + Leaf | = λaa, | ||||||
| + (Branchbs) | = λa.Branch(⊕bs a), | ||||||
| ⊕ Empty | = λaEmpty, | ||||||
| ⊕ (Tconsbbs) | = λa.Tcons(+ba)(⊕bs a). |
| τ1 | := tree → tree, | ||
| τ2 | := tree → tlist. |
| M1 | := λaa, | ||
| M2 | := λbsλgτ2 λa.Branch(g a), | ||
| M3 | := λaEmpty, | ||
| M4 | := λbλbsλfτ1 λgτ2 λa.Tcons(f a)(g a). |
| + | := ℛtree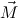 : tree → tree → tree, : tree → tree → tree, | ||
| ⊕ | := ℛtlist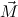 : tlist → tree → tlist. : tlist → tree → tlist. |
To explain the conversion relation, it will be useful to employ the following
notation. Let 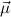 = μ
= μ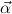
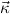 ,
,
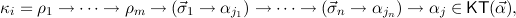
and consider constri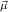
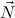 . Then we write
. Then we write 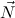 P = N1P ,…,NmP for the parameter
arguments N1ρ1,…,Nmρm and
P = N1P ,…,NmP for the parameter
arguments N1ρ1,…,Nmρm and 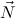 R = N1R,…,NnR for the recursive arguments
Nm+1
R = N1R,…,NnR for the recursive arguments
Nm+1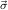 1→μj1,…,Nm+n
1→μj1,…,Nm+n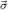 n→μjn, and nR for the number n of recursive arguments.
n→μjn, and nR for the number n of recursive arguments.
We define a conversion relation  ρ between terms of type ρ by
ρ between terms of type ρ by
| (λxM)N |  M[x:=N] M[x:=N] | (1) |
| λx.Mx |  M if x M if x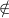 FV(M), M not an abstraction FV(M), M not an abstraction | (2) |
(ℛj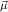 , ,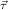 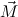 )μj→τj
(constri )μj→τj
(constri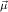 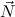 ) ) |  M
i M
i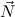 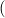 (ℛj
1 (ℛj
1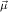 , ,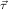 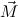 ) ∘ N
1R ) ∘ N
1R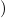 … …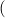 (ℛ
jn (ℛ
jn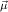 , ,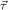 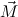 ) ∘ N
nR ) ∘ N
nR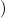 | (3) |
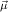 ,
,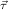 for ℛμj
for ℛμj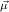 ,
,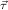 , and ∘ means composition.
, and ∘ means composition.
4.3. Internal representation of constants. Every object constant has the internal representation
| (const | object-or-arity name uninst-type-or-formula subst | ||
| t-deg token-type arrow-types-or-repro-formulas), |
(const Compose (α→β)→(β→γ)→α→γ (α ρ,β ρ,β σ,γ σ,γ τ) ...) τ) ...) | |||||
(const Eq α → α → boole (α finalg) ...) finalg) ...) | |||||
(const E α → boole (α finalg…)) finalg…)) | |||||
| (const Ex-Elim ∃xαP(x) → (∀xα.P(x) → Q) → Q | |||||
(α τ,P(α) τ,P(α) {zτ ∣ A},Q {zτ ∣ A},Q { ∣ B }) ...) { ∣ B }) ...) |
Constructor, accessors and tests for all kinds of constants:
tsubst must be restricted to the type variables in uninst-type. arrow-types-or-repro-formulas are only present for the Rec constants. They are needed for the reproduction case.From these we can define
| (const-to-type const) | |||||
| (const-to-tvars const) |
A constructor is a special constant with no rules. We maintain an association list CONSTRUCTORS assigning to every name of a constructor an association list associating with every type substitution (restricted to the type parameters) the corresponding instance of the constructor. We provide
| (constr-name? string) | |||||
| (constr-name-to-constr name <tsubst>) | |||||
| (constr-name-and-tsubst-to-constr name tsubst), |
For given algebras one can display the associated constructors with their types by calling
| (display-constructors alg-name1 ...). |
We also need procedures recovering information from the string denoting a program constant (via PROGRAM-CONSTANTS):
One can display the program constants together with their current computation and rewrite rules by calling
| (display-program-constants name1 ...). |
To add and remove program constants we use
| (add-program-constant name type <rest>) | |||
| (remove-program-constant symbol); |
To add and remove computation and rewrite rules we have
| (add-computation-rule lhs rhs) | |||
| (add-rewrite-rule lhs rhs) | |||
| (remove-computation-rules-for lhs) | |||
| (remove-rewrite-rules-for lhs). |
To generate our constants with fixed rules we use
| (finalg-to-=-const finalg) | equality | ||||||
| (finalg-to-e-const finalg) | existence | ||||||
| (arrow-types-to-rec-const . arrow-types) | recursion | ||||||
| (ex-formula-and-concl-to-ex-elim-const | |||||||
| ex-formula concl) |
Similarly to arrow-types-to-rec-const we also define the procedure all-formulas-to-rec-const. It will be used in to achieve normalization of proofs via translating them in terms.
[Noch einfügen: arrow-types-to-cases-const und zur Behandlung von Beweisen all-formulas-to-cases-const]