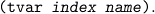[next] [prev] [prev-tail] [tail] [up]

2. Types, with simultaneous free algebras as base types

S:Types

Generally we consider typed theories only. Types are built from type variables and type constants by algebra type formation (alg ρ1…ρn), arrow type formation ρ → σ and product type formation ρ × σ (and possibly other type constructors).

We have type constants atomic, existential, prop and nulltype. They will be used to assign types to formulas. E.g. ∀nn = 0 receives the type nat → atomic, and ∀n,m∃k n + m = k receives the type nat → nat → existential. The type prop is used for predicate variables, e.g. R of arity nat,nat -> prop. Types of formulas will be necessary for normalization by evaluation of proof terms. The type nulltype will be useful when assigning to a formula the type of a program to be extracted from a proof of this formula. Types not involving the types atomic, existential, prop and nulltype are called object types.

Type variable names are alpha,beta…; alpha is provided by default. To have infinitely many type variables available, we allow appended indices: alpha1,alpha2,alpha3… will be type variables. The only type constants are atomic,existential,prop and nulltype.

2.1. Generalitites for substitutions, type substitutions.

SS:GenSubst

Generally, a substitution is a list ((x1 t1)…(xn tn)) of lists of length two, with distinct variables xi and such that for each i, xi is different from ti. It is understood as simultaneous substitution. The default equality is equal?; however, in the versions ending with -wrt (for “with respect to”) one can provide special notions of equality. To construct substitutions we have
(make-substitution args vals)
(make-substitution-wrt arg-val-equal? args vals)
(make-subst arg val)
(make-subst-wrt arg-val-equal? arg val)
empty-subst
Accessing a substitution is done via the usual access operations for association list: assoc and assoc-wrt. We also provide
(restrict-substitution-wrt subst test?)
(restrict-substitution-to-args subst args)
(substitution-equal? subst1 subst2)
(substitution-equal-wrt? arg-equal? val-equal? subst1 subst2)
(subst-item-equal-wrt? arg-equal? val-equal? item1 item2)
(consistent-substitutions-wrt?
arg-equal? val-equal? subst1 subst2)

Composition ϑσ of two substitutions

ϑ = ((x1 s1)…(xm sm)),
σ = ((y1 t1)…(yn tn))
is defined as follows. In the list ((x1 s1σ)…(xm smσ) (y1 t1)…(yn tn)) remove all bindings (xi siσ) with siσ = xi, and also all bindings (yj tj) with yj ∈{x1,…,xn}. It is easy to see that composition is associative, with the empty substitution as unit. We provide
(compose-substitutions-wrt  substitution-proc arg-equal?
arg-val-equal? subst1 subst2)

We shall have occasion to use these general substitution procedures for the following kinds of substitutions

|--------------------|-------|----------------|-------------------| |for------------------|called--|domain--equality-|arg- val-equality-----| |type variables |tsubst |equal? |equal? | |object variables |osubst |equal? |var-term -equal? | |predicate variables |psubst |equal? |pvar-cterm -equal? | |assumption-variables-|asubst--avar=?-----------avar-proof--equal?-- | |

The following substitutions will make sense for a

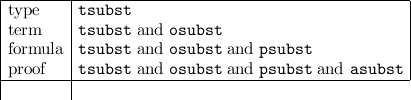
|type----|tsubst------------------------------------| |term |tsubst and osubst | | | | |formula |tsubst and osubst and psubst | |proof---|tsubst--and-osubst-and-psubst-and-asubst--| | |

In particular, for type substitutions tsubst we have

(type-substitute type tsubst)
(type-subst type tvar type1)
(compose-t-substitutions tsubst1 tsubst2)
A display function for type substitutions is
(display-t-substitution tsubst)

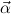2.2. Simultaneous free algebras as base types. We allow the formation of inductively generated types μ⃗α⃗κ, where ⃗α = α1,…,αn is a list of distinct type variables, and ⃗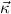κ is a list of “constructor types” whose argument types contain α1,…,αn in strictly positive positions only.

For instance, μα(α,α → α) is the type of natural numbers; here the list (α,α → α) stands for two generation principles: α for “there is a natural number” (the number 0), and α → α for “for every natural number there is another one” (its successor).

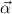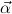Let an infinite supply of type variables α,β be given. Let ⃗α = (αj)j=1,…,m be a list of distinct type variables. Types ρ,σ,τ,μ,ν ∈ Types and constructor types κ ∈ KT(⃗α) are defined inductively as follows.

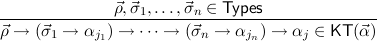--------------⃗ρ,⃗σ1,...,⃗σn-∈-Types--------------- ⃗ρ → (⃗σ1 → αj1) → ⋅⋅⋅ → (⃗σn → αjn) → αj ∈ KT( ⃗α) (n ≥ 0)
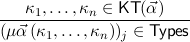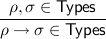---κ1,...,κn ∈-KT(-⃗α)--- (μ⃗α (κ1,...,κn))j ∈ Types (n ≥ 1, j = 1,…,m) -ρ,σ-∈-Types-- ρ → σ ∈ Types
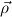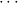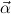Here ⃗ρ is short for a list ρ1,…,ρk (k ≥ 0) of types and ⃗ρ → σ means ρ1 →⋅⋅⋅→ ρk → σ, associated to the right. We shall use μ,ν for types of the form (μ⃗α(κ1,…,κn))j only, and for types ⃗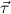τ = (τj)j=1,…,m and a constructor type κ = ⃗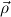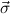ρ → (⃗σ1 → αj1) →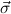⋅⋅⋅→ (⃗σn → αjn) → αj ∈ KT(⃗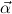α) let
κ[⃗τ ] := ⃗ρ → (⃗σ1 → τj1) → ⋅⋅⋅ → (⃗σn → τjn) → τj.

Examples.

unit := μαα,
boole := μα (α,α),
nat := μα (α,α → α),
ytensor(α1)(α2) := μα.α1 → α2 → α,
ypair(α1)(α2) := μα.(unit → α1) → (unit → α2) → unit → α,
yplus(α1)(α2) := μα.(α1 → α,α2 → α),
list(α1) := μα (α,α1 → α → α),
(tree,tlist) := μ(α,β)(α,β → α,β,α → β → β),
btree := μα (α,α → α → α),
𝒪 := μα (α,α → α,(nat → α) → α),
𝒯0 := nat,
𝒯n+1 := μα (α,(𝒯n → α) → α).
Note that we could have defined our primitive ρ×σ by μα.ρ → σ → α. However, this may lead to complex terms when it comes to extract programs from proofs. Therefore we stick to using ρ × σ as a primitive.

To add and remove names for type variables, we use

(add-tvar-name name1 ...)
(remove-tvar-name name1 ...)
We need a constructor, accessors and a test for type variables.
(make-tvar index name) constructor
(tvar-to-index tvar) accessor
(tvar-to-name tvar) accessor
(tvar? x).
To generate new type variables we use
(new-tvar type)

To introduce simultaneous free algebras we use

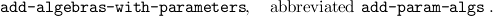
add -algebras- with-parameters, abbreviated add -param-algs .

An example is

(add-param-algs  
  (list "labtree" "labtlist") ’alg-typeop 2  
  ’("LabLeaf" "alpha1=>labtree")  
  ’("LabBranch" "labtlist=>alpha2=>labtree")  
  ’("LabEmpty" "labtlist")  
  ’("LabTcons" "labtree=>labtlist=>labtlist" pairscheme-op))

This simultaneously introduces the two free algebras labtree and labtlist, both finitary, whose constructors are LabLeaf, LabBranch, LabEmpty and LabTcons (written as an infix pair operator, hence right associative). The constructors are introduced as “self-evaluating” constants; they play a special role in our semantics for normalization by evaluation.

In case there are no parameters we use add-algs, and in case there is no need for a simultaneous definition we use add-alg or add-param-alg.

For already introduced algebras we need constructors and accessors

(make-alg name type1 ...)
(alg-form-to-name alg)
(alg-form-to-types alg)
(alg-name-to-simalg-names alg-name)
(alg-name-to-token-types alg-name)
(alg-name-to-typed-constr-names alg-name)
(alg-name-to-tvars alg-name)
(alg-name-to-arity alg-name)
We also provide the tests
(alg-form? x) incomplete test
(alg? x) complete test
(finalg? type) incomplete test
(ground-type? x) incomplete test

We require that there is at least one nullary constructor in every free algebra; hence, it has a “canonical inhabitant”. For arbitrary types this need not be the case, but occasionally (e.g. for general logical problems, like to prove the drinker formula) it is useful. Therefore

(make-inhabited type term1 ...)
marks the optional term as the canonical inhabitant if it is provided, and otherwise creates a new constant of that type, which is taken to be the canonical inhabitant. We also have
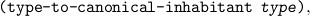
(type-to-canonical -inhabitant type ),

which returns the canonical inhabitant; it is an error to apply this procedure to a non-inhabited type. We do allow non-inhabited types to be able to implement some aspects of [7, 1]

To remove names for algebras we use

(remove-alg-name name1 ...)

Examples. Standard examples for finitary free algebras are the type nat of unary natural numbers, and the type btree of binary trees. The domain ℐnat of unary natural numbers is defined (as in [4]) as a solution to a domain equation.

We always provide the finitary free algebra unit consisting of exactly one element, and boole of booleans; objects of the latter type are (cf. loc. cit.) true, false and families of terms of this type, and in addition the bottom object of type boole.

Tests:

(arrow-form? type)
(star-form? type)
(object-type? type)

We also need constructors and accessors for arrow types

(make-arrow arg-type val-type) constructor
(arrow-form-to-arg-type arrow-type) accessor
(arrow-form-to-val-type arrow-type) accessor
and star types
(make-star type1 type2) constructor
(star-form-to-left-type star-type) accessor
(star-form-to-right-type star-type) accessor.
For convenience we also have
(mk-arrow type1 ... type)
(arrow-form-to-arg-types type <n>) all (first n) argument types
(arrow-form-to-final-val-type type) type of final value.
To check and to display a type we have
(type? x)
(type-to-string type).

Implementation. Type variables are implemented as lists:

(tvar index name).

[next] [prev] [prev-tail] [front] [up]