|
|
Intro
We now describe in more details some of these features.
1.1. Simultaneous free algebras. A free algebra is given by constructors, for instance zero and successor for the natural numbers. We want to treat other data types as well, like lists and binary trees. When dealing with inductively defined sets, it will also be useful to explicitely refer to the generation tree. Such trees are quite often countably branching, and hence we allow infinitary free algebras from the outset.
The freeness of the constructors is expressed by requiring that their ranges are disjoint and that they are injective. Moreover, we view the free algebra as a domain and require that its bottom element is not in the range of the constructors. Hence the constructors are total and non-strict. For the notion of totality cf. [12, Chapter 8.3].
In our intended semantics we do not require that every semantic object is the denotation of a closed term, not even for finitary algebras. One reason is that for normalization by evaluation (cf. [4]) we want to allow term families in our semantics.
To make a free algebra into a domain and still have the constructors injective and with disjoint ranges, we model e.g. the natural numbers as shown in Figure 1.
Notice that for more complex algebras we usually need many more “infinite” elements; this is a consequence of the closure of domains under suprema. To make dealing with such complex structures less annoying, we will normally restrict attention to the total elements of a domain, in this case – as expected – the elements labelled 0, S0, S(S0) etc.
1.2. Partial continuous functionals. As already mentioned, the (mathematically correct) domains of computable functionals have been identified by Scott and Ershov as the partial continuous functionals; cf. [12]. Since we want to deal with computable functionals in our theory, we consider it as mandatory to accommodate their domains. This is also true if one is interested in total functionals only; they have to be treated as particular partial continuous functionals. We will make use of predicate constants Totalρ with the total functionals of type ρ as the intended meaning. To make formal arguments with quantifiers relativized to total objects more managable, we use a special sort of variables intended to range over such objects only. For example, n0,n1,n2,…,m0,… range over total natural numbers, and nˆ0,nˆ1,nˆ2,… are general variables. This amounts to an abbreviation of
∀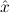 .Totalρ( .Totalρ(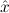 ) → A ) → A | by | ∀xA, | |||||
∃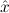 .Totalρ( .Totalρ(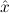 ) ∧ A ) ∧ A | by | ∃xA. |
1.3. Primitive recursion, computable functionals. The elimination constants corresponding to the constructors are called primitive recursion operators ℛ. They are described in detail in Section 4. In this setup, every closed term reduces to a numeral.
However, we shall also use constants for rather arbitrary computable functionals, and axiomatize them according to their intended meaning by means of rewrite rules. An example is the general fixed point operator fix, which is axiomatized by fixF = F(fixF). Clearly then it cannot be true any more that every closed term reduces to a numeral. We may have non-terminating terms, but this just means that not always it is a good idea to try to normalize a term.
An important consequence of admitting non-terminating terms is that our notion of proof is not decidable: when checking e.g. whether two terms are equal we may run into a non-terminating computation. But we still have semi-decidability of proofs, i.e., an algorithm to check the correctness of a proof that can only give correct results, but may not terminate. In practice this is sufficient.
To avoid this somewhat unpleasant undecidability phenomenon, we may also view our proofs as abbreviated forms of full proofs, with certain equality arguments left implicit. If some information sufficient to recover the full proof (e.g. for each node a bound on the number of rewrite steps needed to verify it) is stored as part of the proof, then we retain decidability of proofs.
1.4. Decidable predicates, axioms for predicates. As already mentioned, decidable predicates are viewed via boolean valued functions, hence the rewrite mechanism applies to them as well.
Equality is decidable for finitary algebras only; infinitary algebras are to be treated similarly to arrow types. For infinitary algebras (extensional) equality is a predicate constant, with appropriate axioms. In a finitary algebra equality is a (recursively defined) program constant. Similarly, existence (or totality) is a decidable predicate for finitary algebras, and given by predicate constants Totalρ for infinitary algebras as well as composed types. The axioms are listed in Subsection 8.2 of Section 8.
1.5. Minimal logic, proof transformation. For generalities about minimal logic cf. [13]. A concise description of the theory behind the present implementation can be found in “Minimal Logic for Computable Functions” which is available on the Minlog page www.minlog-system.de.
1.6. Comparison with Coq and Isabelle.
SS:Coq
The Isabelle/HOL system of Paulson and Nipkow has its roots in Church’s theory of simple types and Hilbert’s Epsilon calculus. It is an inherently classical system; however, since many proofs in fact use constructive arguments, in is conceivable that program extraction can be done there as well. This has been explored by Berghofer in his thesis [6].
Compared with the Minlog system, the following points are of interest.