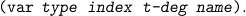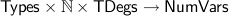
Variables
In most cases we need to argue about existing (i.e. total) objects only. For the notion of totality we have to refer to [12, Chapter 8.3]; particularly relevant here is exercise 8.5.7. To make formal arguments with quantifiers relativized to total objects more managable, we use a special sort of variables intended to range over such objects only. For example, n0,n1,n2,…,m0,… range over total natural numbers, and nˆ0,nˆ1,nˆ2,… are general variables. We say that the degree of totality for the former is 1, and for the latter 0.
n,m for variables of type nat), we use
| (add-var-name name1 ... type) | |||
| (remove-var-name name1 ... type) | |||
| (default-var-name type). |
We need a constructor, accessors and tests for variables.
equal? is a valid test for equality of variables. Moreover, it is guaranteed that parsing a displayed variable reproduces the variable; the converse need not be the case (we may want to convert it into some canonical form).For convenience we have the function
| (mk-var type <index> <t-deg> <name>). |
| (default-var-name type) |
Using the empty string as the name, we can create so called numerated variables. We further require that we can test whether a given variable belongs to those special ones, and that from every numerated variable we can compute its index:
| (numerated-var? var) | |||
| (numerated-var-to-index numerated-var). |
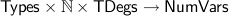
with inverses var-to-type, numerated-var-to-index and var-to-t-deg.
Although these functions look like an ad hoc extension of the interface that is convenient for normalization by evaluation, there is also a deeper background: these functions can be seen as the “computational content” of the well-known phrase “we assume that there are infinitely many variables of every type”. Giving a constructive proof for this statement would require to give infinitely many examples of variables for every type. This of course can only be done by specifying a function (for every type) that enumerates these examples. To make the specification finite we require the examples to be given in a uniform way, i.e. by a function of two arguments. To make sure that all these examples are in fact different, we would have to require make-var to be injective. Instead, we require (classically equivalent) make-var to be a bijection on its image, as again, this can be turned into a computational statement by requiring that a witness (i.e. an inverse function) is given.
Finally, as often the exact knowledge of infinitely many variables of every type is not needed we require that, either by using the above functions or by some other form of definition, functions
| (type-to-new-var type) | |||
| (type-to-new-partial-var type) |
Occasionally we may want to create a new variable with the same name (and degree of totality) as a given one. This is useful e.g. for bound renaming. Therefore we supply
| (var-to-new-var var). |
Implementation. Variables are implemented as lists: