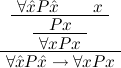
Proof
9.1. Constructors and accessors. We have constructors, accessors and tests for assumption variables
| (make-proof-in-avar-form avar) | constructor | ||||||
| (proof-in-avar-form-to-avar proof) | accessor, | ||||||
| (proof-in-avar-form? proof) | test, |
| (make-proof-in-aconst-form aconst) | constructor | ||||||
| (proof-in-aconst-form-to-aconst proof) | accessor | ||||||
| (proof-in-aconst-form? proof) | test, |
| (make-proof-in-imp-intro-form avar proof) | constructor | ||||||
| (proof-in-imp-intro-form-to-avar proof) | accessor | ||||||
| (proof-in-imp-intro-form-to-kernel proof) | accessor | ||||||
| (proof-in-imp-intro-form? proof) | test, |
| (make-proof-in-imp-elim-form proof1 proof2) | constructor | ||||||
| (proof-in-imp-elim-form-to-op proof) | accessor | ||||||
| (proof-in-imp-elim-form-to-arg proof) | accessor | ||||||
| (proof-in-imp-elim-form? proof) | test, |
| (make-proof-in-and-intro-form proof1 proof2) | constructor | ||||||
| (proof-in-and-intro-form-to-left proof) | accessor | ||||||
| (proof-in-and-intro-form-to-right proof) | accessor | ||||||
| (proof-in-and-intro-form? proof) | test, |
| (make-proof-in-all-intro-form var proof) | constructor | ||||||
| (proof-in-all-intro-form-to-var proof) | accessor | ||||||
| (proof-in-all-intro-form-to-kernel proof) | accessor | ||||||
| (proof-in-all-intro-form? proof) | test, |
| (make-proof-in-all-elim-form proof term) | constructor | ||||||
| (proof-in-all-elim-form-to-op proof) | accessor | ||||||
| (proof-in-all-elim-form-to-arg proof) | accessor | ||||||
| (proof-in-all-elim-form? proof) | test |
| (mk-proof-in-intro-form x1 ... proof) | |||||
| (mk-proof-in-elim-form proof arg1 ...) | |||||
| (proof-in-intro-form-to-kernel-and-vars proof) | |||||
| (proof-in-elim-form-to-final-op proof) | |||||
| (proof-in-elim-form-to-args proof). |
| (mk-proof-in-and-intro-form proof proof1 ...) |
In our setup there are axioms rather than rules for the existential quantifier. However, sometimes it is useful to construct proofs as if an existence introduction rule would be present; internally then an existence introduction axiom is used.
| (make-proof-in-ex-intro-form term ex-formula proof-of-inst) | |||||
| (mk-proof-in-ex-intro-form . | |||||
| terms-and-ex-formula-and-proof-of-inst) |
Moreover we need
| (context-to-vars context) | |||||
| (context-to-avars context) | |||||
| (context=? context1 context2). |
9.2. Normalization. Normalization of proofs will be done by reduction to normalization of terms. (1) Construct a term from the proof. To do this properly, create for every free avar in the given proof a new variable whose type comes from the formula of the avar; store this information. Note that in this construction one also has to create new variables for the bound avars. Similary to avars we have to treat assumption constants which are not axioms, i.e. theorems or global assumptions. (2) Normalize the resulting term. (3) Reconstruct a normal proof from this term, the end formula and the stored information. – The critical variables are carried along for efficiency reasons.
To assign recursion constants to induction constants, we need to associate type variables with predicate variables, in such a way that we can later refer to this assignment. Therefore we carry along a procedure pvar-to-tvar which remembers the assignment done so far (cf. make-rename).
Due to our distinction between general variables xˆ0,xˆ1,xˆ2,… and variables x0,x1,x2,… intended to range over existing (i.e. total) objects only, η-conversion of proofs cannot be done via reduction to η-conversion of terms. To see this, consider the proof
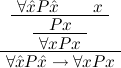
The proof term is λuλx.ux. If we η-normalize this to λuu, the proven formula
would be all ∀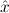 P
P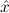 →∀
→∀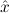 P
P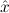 . Therefore we split nbe-normalize-proof into
nbe-normalize-proof-without-eta and proof-to-eta-nf.
. Therefore we split nbe-normalize-proof into
nbe-normalize-proof-without-eta and proof-to-eta-nf.
Moreover, for a full normalization of proofs (including permutative conversions) we need a preprocessing step that η-expands each ex-elim axiom such that the conclusion is atomic or existential.
We need the following functions.
| (proof-and-genavar-var-alist-to-pterm pvar-to-tvar proof) | |||||
| (npterm-and-var-genavar-alist-and-formula-to-proof | |||||
| npterm var-genavar-alist crit formula) | |||||
| (elim-npterm-and-var-genavar-alist-to-proof | |||||
| npterm var-genavar-alist crit). |
9.3. Substitution. In a proof we can substitute
It is assumed that subst only affects those vars whose type is not changed by tsubst, psubst only affects those predicate variables whose arity is not changed by tsubst, and that asubst only affects those assumtion variabless whose formula is not changed by tsubst, subst and psubst.
In the abstraction cases of the recursive definition, the abstracted variable (or assumption variable) may need to be renamed. However, its type (or formula) can be affected by tsubst (or tsubst, subst and psubst). Then the renaming cannot be made part of subst (or asubst), because the condition above would be violated. Therefore we carry along procedures rename renaming variables and arename for assumption variables, which remember the renaming done so far.
All these substitutions can be packed together, as an argument topasubst for proof-substitute.
| (proof-substitute proof topasubst) |
| (proof-subst proof arg val) |
The procedure expand-theorems expects a proof and a test whether a string denotes a theorem to be replaced by its proof. The result is the (normally quite long) proof obtained by replacing the theorems by their saved proofs.
| (expand-theorems proof name-test?) |
9.4. Display. There are many ways to display a proof. We normally use display-proof for a linear representation, showing the formulas and the rules used. When we in addition want to check the correctness of the proof, we can use check-and-display-proof.
However, we also provide a readable type-free lambda expression via (proof-to-expr proof).
To display proofs we use the following functions. In case the optional proof argument is not present, the current proof of an interactive proof development is taken instead.
| (display-proof . opt-proof) | abbreviated dp | ||||||
| (check-and-display-proof . opt-proof) | abbreviated cdp | ||||||
| (display-pterm . opt-proof) | abbreviated dpt | ||||||
| (display-proof-expr . opt-proof) | abbreviated dpe |
| (display-normalized-proof . opt-proof) | abbreviated dnp | ||||||
| (display-normalized-pterm . opt-proof) | abbreviated dnpt | ||||||
| (display-normalized-proof-expr . opt-proof) | abbreviated dnpe |
9.5. Classical logic.
(proof-of-stab-at formula) generates a proof of ((A → F) → F) → A. For
F, T one takes the obvious proof, and for other atomic formulas the proof using
cases on booleans. For all other prime or existential formulas one takes an
instance of the global assumption Stab: ((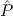 → F) → F) →
→ F) → F) →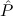 . Here the
argument formula must be unfolded. For the logical form of falsity we take
(proof-of-stab-log-at formula), and similary for ex-falso-quodlibet we
provide
. Here the
argument formula must be unfolded. For the logical form of falsity we take
(proof-of-stab-log-at formula), and similary for ex-falso-quodlibet we
provide
| (proof-of-efq-at formula) | |||||
| (proof-of-efq-log-at formula) |
With rm-exc we can transform a proof involving classical existential quantifiers in another one without, i.e. in minimal logic. The Exc-Intro and Exc-Elim theorems are replaced by their proofs, using expand-theorems.