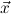i.A[x:=x1i] →
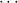→ A[x:=xki] → A[x:=ci
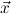i] are generated.
(ind t) expects a goal A[x:=t]. It computes the algebra ρ as type of the term
t. Then again n new goals ∀
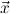i.A[x:=x1i] →
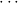→ A[x:=xki] → A[x:=ci
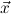i] are
generated.
Pproof
10.1. Partial proofs. A partial proof is a proof with holes, i.e. special assumption variables (called goal variables) v, v1, v2 ...whose formulas must be closed. We assume that every goal variable v has a single occurrence in the proof. We then select a (not necessarily maximal) subproof vx1...xn with distinct object or assumption variables x1...xn. Such a subproof is called a goal. When interactively developing a partial proof, a goal vx1...xn is replaced by another partial proof, whose context is a subset of x1...xn (i.e. the context of the goal with v removed).
To gain some flexibility when working on our goals, we do not at each step of an interactive proof development traverse the partial proof searching for the remaining goals, but rather keep a list of all open goals together with their numbers as we go along. We maintain a global variable PPROOF-STATE containing a list of three elements: (1) num-goals, an alist of entries (number goal drop-info hypname-info), (2) proof and (3) maxgoal, the maximal goal number used.
At each stage of an interactive proof development we have access to the current proof and the current goal by executing
| (current-proof) | |||||
| (current-goal) |
10.2. Interactive theorem proving. For interactively building proofs we need
We list some commands for interactively building proofs.
10.2.1. set-goal. An interactive proof starts with (set-goal formula), i.e. with setting a goal. Here formula should be closed; if it is not, universal quantifiers are inserted automatically.
10.2.2. normalize-goal. (normalize-goal goal) (abbreviated ng) replaces every formula in the goal by its normal form.
10.2.3. assume. With (assume x1 ...) we can move universally quantified variables and hypotheses into the context. The variables must be given names (known to the parser as valid variable names for the given type), and the hypotheses should be identified by numbers or strings.
10.2.4. use. In (use x . elab-path-and-terms), x is
The optional elab-path-and-terms is a list consisting of symbols left or right, giving directions in case the used formula contains conjunctions, and of terms. The universal quantifiers of the used formula are instantiated (via pattern-unify) with appropriate terms in case a conclusion has the form of the goal. The terms provided are substituted for those variables that cannot be instantiated by pattern unification (e.g. using ∀x.Px →⊥ for the goal ⊥). For the instantiated premises new goals are created.
10.2.5. use-with. This is a more verbose form of use, where the terms are not inferred via unification, but have to be given explicitely. Also, for the instantiated premises one can indicate how they are to come about. So in (use-with x . x-list), x is as in use, and x-list is a list consisting of
Notice that new free variables not in the ordered context can be introduced in use-with. They will be present in the newly generated goals. The reason is that proofs should be allowed to contain free variables. This is necessary to allow logic in ground types where no constant is available (e.g to prove ∀xPx →∀x¬Px →⊥).
Notice also that there are situations where use-with can be applied but use can not. For an example, consider the goal P(S(k + l)) with the hypothesis ∀lP(k + l) in the context. Then use cannot find the term Sl by matching; however, applying use-with to the hyposthesis and the term Sl succeeds (since k + Sl and S(k + l) have the same normal form).
10.2.6. inst-with. inst-with does for forward chaining the same as use-with for backward chaining. It replaces the present goal by a new one, with one additional hypothesis obtained by instantiating a previous one. Notice that this effect could also be obtained by cut. In (inst-with x . x-list), x is
and x-list is a list consisting of
10.2.7. inst-with-to. inst-with-to expects a string as its last argument, which is used (via name-hyp) to name the newly introduced instantiated hypothesis.
10.2.8. cut. The command (cut A) replaces the goal B by the two new goals A and A → B.
10.2.9. strip. To move (all or n) universally quantified variables and hypotheses of the current goal into the context, we uns the command (strip) or (strip n).
10.2.10. drop. In (drop . x-list), x-list is a list of numbers or strings identifying hypotheses from the context. A new goal is created, which differs from the previous one only in display aspects: the listed hypotheses are hidden (but still present). If x-list is empty, all hypotheses are hidden.
10.2.11. name-hyp. The command name-hyp expects an index i and a string. Then a new goal is created, which differs from the previous one only in display aspects: the string is used to label the ith hypothesis.
10.2.12. split. The command (split) expects a conjunction A ∧ B as goal and splits it into the two new goals A and B.
10.2.13. get. To be able to work on a goal different from that on top of the goal stack, we have have to move it up using (get n).
10.2.14. undo. With (undo . n), the last n steps of an interactive proof can be made undone. (undo) has the same effect as (undo 1).
10.2.15. ind. (ind) expects a goal ∀xρA with ρ an algebra. Let
c1,…,cn be the constructors of the algebra ρ. Then n new goals
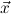∀i.A[x:=x1i] →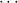→ A[x:=xki] → A[x:=ci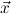i] are generated.
(ind t) expects a goal A[x:=t]. It computes the algebra ρ as type of the term
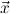t. Then again n new goals ∀i.A[x:=x1i] →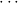→ A[x:=xki] → A[x:=ci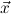i] are
generated.
10.2.16. simind. (simind all-formula1 ...) also expects a goal ∀xρA with ρ an algebra. Then we have to provide the other all formulas to be proved simultaneously with the given one.
10.2.17. intro. (intro i . terms) expects as goal an inductively defined predicate. The i-th introduction axiom for this predicate is applied, via use (hence terms may have to be provided).
10.2.18. elim. (elim) expects a goal I(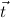
) → A[
:=
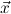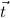]. Then the (strengthened)
clauses are generated as new goals, via use-with.
10.2.19. ex-intro. In (ex-intro term), the user provides a term to be used for the present (existential) goal. (exnc-intro x) works similarly for the exnc-quanhtifier.
10.2.20. ex-elim. In (ex-elim x), x is
Let ∃yA be the existential formula identified by x. The user is then asked to provide a proof for the present goal, assuming that a y satisfying A is available. (exnc-elim x) works similarly for the exnc-quanhtifier.
10.2.21. by-assume-with. Suppose we are proving a goal G from an existential hypothesis ExHyp: ∃yA. Then the natural way to use this hypothesis is to say “by ExHyp assume we have a y satisfying A”. Correspondingly we provide (by-assume-with x y u). Here x – as in ex-elim – identifies an existential hypothesis, and we assume (i.e. add to the context) the variable y and – with label u – the kernel A. (by-assume-with x y u) is implemented by the sequence (ex-elim x), (assume y u), (drop x). by-exnc-assume-with works similarly for the exnc-quantifier.
10.2.22. cases. (cases) expects a goal ∀xρA with ρ an algebra. Assume that
c1,…,cn are the constructors of the algebra ρ. Then n new (simplified) goals
∀
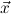iA[x:=ci
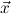i] are generated.
(cases t) expects a goal A[x:=t]. It computes the algebra ρ as type of the
term t. Then again n new goals ∀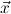
iA[x:=ci
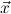i] are generated.
(cases ’auto) expects an atomic goal and checks whether its boolean kernel contains an if-term whose test is neither an if-term nor contains bound variables. With the first such test (cases test) is called.
10.2.23. casedist. (casedist t) replaces the goal A containing a boolean term t by two new goals (atom t) → A[t:=tt] and ((atom t) → ff) → A[t:=ff].
10.2.24. simp. In (simp opt-dir x . elab-path-and-terms), the optional argument opt-dir is either the string “<-” or missing. x is
The optional elab-path-and-terms is a list consisting of symbols left or right, giving directions in case the used formula contains conjunctions, and of terms. The universal quantifiers of the used formula are instantiated with appropriate terms to match a part of the goal. The terms provided are substituted for those variables that cannot be inferred. For the instantiated premises new goals are created. This generates a used formula, which is to be an atom, a negated atom or t ≈ s. If it as a (negated) atom, it is checked whether the kernel or its normal form is present in the goal. If so, it is replace by T (or F). If it is an equality t = s or t ≈ s with t or its normal form present in the goal, t is replaced by s. In case “<-” exchange t and s.
10.2.25. simp-with. This is a more verbose form of simp, where the terms are not inferred via matching, but have to be given explicitely. Also, for the instantiated premises one can indicate how they are to come about. So in (simp-with opt-dir x . x-list), opt-dir and x are as in simp, and x-list is a list consisting of
10.2.26. min-pr. In (min-pr x measure), x is
The result is a new implicational goal, whose premise provides the (classical) existence of instances with least measure.
10.2.27. exc-intro. In (exc-intro terms), the user provides terms to be used for the present (classical existential) goal.
10.2.28. exc-elim. In (exc-elim x), x is
Let ∃ca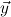
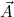or ∃cl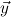
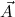be the classical existential formula identified by x. The user is
then asked to provide a proof for the present goal, assuming that terms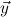 
satisfying 
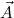are available.
10.2.29. pair-elim. In (pair-elim), a goal ∀pP(p) is replaced by the new goal ∀x1,x2P(〈x1,x2〉).