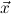 ∃
∃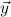 ∀
∀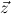 , with distinct variables. We call
, with distinct variables. We call  the signature variables,
the signature variables, 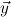 the flexible variables and
the flexible variables and 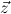 the forbidden variables of Q,
and write Q∃ for the existential part ∃
the forbidden variables of Q,
and write Q∃ for the existential part ∃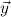 of Q.
of Q.
Following Miller [10] and Berger, we have implemented a proof search algorithm for minimal logic. To enforce termination, every assumption can only be used a fixed number of times.
We begin with a short description of the theory involved.
Q always denotes a ∀∃∀-prefix, say ∀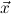 ∃
∃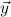 ∀
∀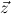 , with distinct variables. We call
, with distinct variables. We call 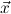 the signature variables,
the signature variables, 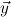 the flexible variables and
the flexible variables and 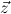 the forbidden variables of Q,
and write Q∃ for the existential part ∃
the forbidden variables of Q,
and write Q∃ for the existential part ∃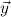 of Q.
of Q.
Q-terms are inductively defined by the following clauses.
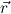 are
Q-terms, then u
are
Q-terms, then u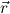 is a Q-term.
is a Q-term.
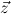 from
Q, y
from
Q, y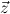 is a Q-term.
is a Q-term.
Explicitely, r is a Q-term iff all its free variables are in Q, and for every subterm y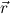 of r with y free in r and flexible in Q, the
of r with y free in r and flexible in Q, the 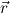 are distinct variables either
λ-bound in r (such that y
are distinct variables either
λ-bound in r (such that y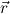 is in the scope of this λ) or else forbidden in
Q.
is in the scope of this λ) or else forbidden in
Q.
Q-goals and Q-clauses are simultaneously defined by
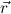 are Q-terms, then P
are Q-terms, then P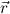 is a Q-goal as well as a Q-clause.
is a Q-goal as well as a Q-clause.
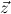 ] is a ∀
] is a ∀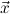 ∃
∃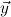 ,Y ∀
,Y ∀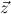 -clause, then ∀yD is a ∀
-clause, then ∀yD is a ∀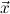 ∃
∃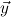 ∀
∀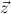 -clause.
-clause.Explicitely, a formula A is a Q-goal iff all its free variables are in Q, and for every
subterm y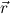 of A with y either existentially bound in A (with y
of A with y either existentially bound in A (with y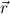 in the scope) or
else free in A and flexible in Q, the
in the scope) or
else free in A and flexible in Q, the 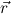 are distinct variables either λ- or universally
bound in A (such that y
are distinct variables either λ- or universally
bound in A (such that y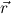 is in the scope) or else free in A and forbidden in
Q.
is in the scope) or else free in A and forbidden in
Q.
A Q-sequent has the form 𝒫⇒ G, where 𝒫 is a list of Q-clauses and G is a Q-goal.
A Q-substitution is a substitution of Q-terms.
A unification problem 𝒰 consists of a ∀∃∀-prefix Q and a conjunction C of
equations between Q-terms of the same type, i.e. ∧
∧
i=1nri = si. We may assume
that each such equation is of the form λ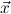 r = λ
r = λ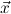 s with the same
s with the same 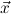 (which may be
empty) and r,s of ground type.
(which may be
empty) and r,s of ground type.
A solution to such a unification problem 𝒰 is a Q-substitution ϕ such that for
every i, riϕ = siϕ holds (i.e. riϕ and siϕ have the same normal form). We
sometimes write C as 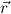 =
= 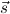 , and (for obvious reasons) call it a list of unification
pairs.
, and (for obvious reasons) call it a list of unification
pairs.
We work with lists of sequents instead of single sequents; they all are Q-sequents for the same prefix Q. One then searches for a Q-substitution ϕ and proofs of the ϕ-substituted sequents. intro-search takes the first sequent and extends Q by all universally quantified variables x1…. It then calls select, which selects (using or) a fitting clause. If one is found, a new prefix Q′ (raising the new flexible variables) is formed, and the n (≥ 0) new goals with their clauses (and also all remaining sequents) are substituted with star∘ ρ, where star is the “raising” substitution and ρ is the mgu. For this constellation intro-search is called again. In case of success, one obtains a Q′-substitution ϕ′ and proofs of the star∘ ρ ∘ ϕ′ -substituted new sequents. Let ϕ := (ρ ∘ ϕ′)↾Q∃, and take the first n proofs of these to build a proof of the ϕ-substituted (first) sequent originally considered by intro-search.
Compared with Miller [10], we make use of several simplifications, optimizations and extensions, in particular the following.
(search m (name1 m1) ...) expects for m a default value for multiplicity (i.e. how often assumptions are to be used), for name1 …
and for m1 ...multiplicities (positive integers for global assumptions or theorems). A search is started for a proof of the goal formula from the given hypotheses with the given multiplicities and in addition from the other hypotheses (but not any other global assumptions or theorems) with m or mult-default. To exclude a hypothesis from being tried, list it with multiplicity 0.