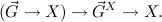
Classical
A formula is relevant if it ends with (logical) falsity. Definite and goal formulas are defined by a simultaneous recursion, as in [3].
| (atr-relevant? formula) | |||||
| (atr-definite? formula) | |||||
| (atr-goal? formula) |
| ND: ((D →⊥) → X) → DX | for D relevant | ||||||
| MD: D → DX | |||||||
| KG: G → GX | for G irrelevant | ||||||
| HG: GX → (G → X) → X |
| (atr-rel-definite-proof formula) | |||||
| (atr-arb-definite-proof formula) | |||||
| (atr-irrel-goal-proof formula) | |||||
| (atr-arb-goal-proof formula) |
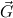 = G1,…,Gn we can derive in minimal logic augmented with a special predicate
variable X
= G1,…,Gn we can derive in minimal logic augmented with a special predicate
variable X
In our implementation this function is called
| (atr-goals-to-x-proof goal1 ...) |
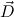 and goal formulas
and goal formulas 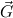 we can derive in minimal
logic
we can derive in minimal
logic
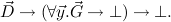
Then we can also derive in intuitionistic logic augmented with the special predicate variable X
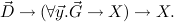
In particular, substitution of the formula
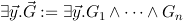
for X yields a derivation in intuitionistic logic of
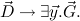
This is done by
| (atr-min-excl-proof-to-x-proof min-excl-proof) | |||||
| (atr-min-excl-proof-to-intuit-ex-proof min-excl-proof) |