13. Extracted terms
We assign to every formula A an object τ(A) (a type or the symbol
nulltype). τ(A) is intended to be the type of the program to be extracted from
a proof of A. This is done by
| (formula-to-et-type formula) | | | | |
In formula-to-et-type we assign type variables to the predicate variables.
For to be able to later refer to this assignment, we use a global variable
PVAR-TO-TVAR-ALIST, which memorizes the assigment done so far. Later
reference is necessary, because such type variables will appear in extracted
programs of theorems involving predicate variables, and in a given development
there may be many auxiliary lemmata containing the same predicate variable. A
fixed pvar-to-tvar refers to and updates PVAR-TO-TVAR-ALIST.
When we want to execute the program, we have to replace the constant cL
corresponding to a lemma L by the extracted program of its proof, and the
constant cGA corresponding to a global assumption GA by an assumed extracted
term to be provided by the user. This can be achieved by adding computation
rules for cL and cGA. We can be rather flexible here and enable/block rewriting
by using animate/deanimate as desired. Notice that the type of the extracted
term provided for a cGA must be the extracted type of the assumed formula.
When predicate variables are present, one must use the type variables assigned to
them in PVAR-TO-TVAR-ALIST.
| (animate thm-or-ga-name . opt-eterm) | | | |
|
| (deanimate thm-or-ga-name) | | | | |
We can define, for a given derivation M of a formula A with τ(A)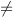 nulltype,
its extracted term (or extracted program) et(M) of type τ(A). We also need
extracted terms for the axioms. For induction we take recursion, for the
proof-by-cases axiom we take the cases-construct for terms; for the other axioms
the extracted terms are rather clear. Term extraction is implemented
by
nulltype,
its extracted term (or extracted program) et(M) of type τ(A). We also need
extracted terms for the axioms. For induction we take recursion, for the
proof-by-cases axiom we take the cases-construct for terms; for the other axioms
the extracted terms are rather clear. Term extraction is implemented
by
| (proof-to-extracted-term proof) | | | | |
It is also possible to give an internal proof of soundness. This can be done
by
| (proof-to-soundness-proof proof) | | | | |
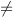 nulltype,
its extracted term (or extracted program) et(M) of type τ(A). We also need
extracted terms for the axioms. For induction we take recursion, for the
proof-by-cases axiom we take the cases-construct for terms; for the other axioms
the extracted terms are rather clear. Term extraction is implemented
by
nulltype,
its extracted term (or extracted program) et(M) of type τ(A). We also need
extracted terms for the axioms. For induction we take recursion, for the
proof-by-cases axiom we take the cases-construct for terms; for the other axioms
the extracted terms are rather clear. Term extraction is implemented
by