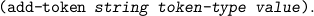
Reading
| (py string) | for parsing types | ||||||
| (pv string) | for parsing variables | ||||||
| (pt string) | for parsing terms | ||||||
| (pf string) | for parsing formulas |
The conversion occurs in two steps: lexical analysis and parsing.
14.1. Lexical analysis. In this stage the string is brocken into short sequences, called tokens.
A token can be one of the following:
For example: abc, ABC and A are alphabetic symbols, 123, 0123 and 7 are numbers, ( is a punctuation mark, and <=, +, and #:-ˆ are special symbols.
Tokens are always character sequences of maximal length belonging to one of the above categories. Therefore fx is a single alphabetic symbol not two and likewise <+ is a single special symbol. The sequence alpha<=(-x+z), however, consists of the 8 tokens alpha, <=, (, -, x, +, z, and ). Note that the special symbols <= and - are separated by a punctuation mark, and the alphabetic symbols x and z are separated by the special symbol +.
If two alphabetic symbols, two special symbols, or two numbers follow each other they need to be separated by white space (spaces, newlines, tabs, formfeeds, etc.). Except for a few situations mentioned below, whitespace has no significance other than separating tokens. It can be inserted and removed between any two tokens without affecting the significance of the string.
Every token has a token type, and a value. The token type is one of the following: number, var-index, var-name, const, pvar-name, predconst, type-symbol, pscheme-symbol, postfix-op, prefix-op, binding-op, add-op, mul-op, rel-op, and-op, or-op, imp-op, pair-op, if-op, postfix-jct, prefix-jct, and-jct, or-jct, tensor-jct, imp-jct, quantor, dot, hat, underscore, comma, semicolon, arrow, lpar, rpar, lbracket, rbracket.
The possible values for a token depend on the token type and are explained below.
New tokens can be added using the function
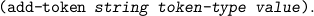
The inverse is the function
A list of all currently defined tokens sorted by token types can be obtained by the function
14.2. Parsing. The second stage, parsing, extracts structure form the sequence of tokens.
Types. Type-symbols are types; the value of a type-symbol must be a type. If σ and τ are types, then σ;τ is a type (pair type) and σ=>τ is a type (function type). Parentheses can be used to indicate proper nesting. For example boole is a predefined type-symbol and hence, (boole;boole)=>boole is again a type. The parentheses in this case are not strictly necessary, since ; binds stronger than =>. Both operators associate to the right.
Variables. Var-names are variables; the value of a var-name token must be a pair consisting of the type and the name of the variable (the same name string again! This is not nice and may be later, we find a way to give the parser access to the string that is already implicit in the token). For example to add a new boolean variable called “flag”, you have to invoke the function (add-token "flag" ’var-name (cons ’boole "flag")). This will enable the parser to recognize “flag3”, “flagˆ”, or “flagˆ14” as well.
Further, types, as defined above, can be used to construct variables.
A variable given by a name or a type can be further modified. If it is followed by a ˆ, a partial variable is constructed. Instead of the ˆ a _ can be used to specify a total variable.
Total variables are the default and therefore, the _ can be omitted.
As another modifier, a number can immediately follow, with no whitespace in between, the ˆ or the _, specifying a specific variable index.
In the case of indexed total variables given by a variable name or a type symbol, again the _ can be omitted. The number must then follow, with no whitespace in between, directly after the variable name or the type.
Note: This is the only place where whitespace is of any significance in the input. If the ˆ, _, type name or variable name is separated from the following number by whitespace, this number is no longer considered to be an index for that variable but a numeric term in its own right.
For example, assuming that p is declared as a variable of type boole, we have:
Terms are built from atomic terms using application and operators.
An atomic term is one of the following: a constant, a variable, a number, a conditional, or any other term enclosed in parentheses.
Constants have const as token type, and the respective term in internal form as value. There are also composed constants, so-called constant schemata. A constant schema has the form of the name of the constant schema (token type constscheme) followed by a list of types, the whole thing enclosed in parentheses. There are a few built in constant schemata: (Rec <typelist>) is the recursion over the types given in the type list; (EQat <type>) is the equality for the given type; (Eat <type>) is the existence predicate for the given type. The constant schema EQat can also be written as the relational infix operator =; the constant schemata Eat can also be written as the prefix operator E.
For a number, the user defined function make-numeric-term is called with the number as argument. The return value of make-numeric-term should be the internal term representation of the number.
To form a conditional term, the if operator if followed by a list of atomic terms is enclosed in square brackets. Depending on the constructor of the first term, the selector, a conditional term can be reduced to one of the remaining terms.
From these atomic terms, compound terms are built not only by application but also using a variety of operators, that differ in binding strength and associativity.
Postfix operators (token type postfix-op) bind strongest, next in binding strength are prefix operators (token type prefix-op), next come binding operators (token type binding-op).
A binding operator is followed by a list of variables and finally a term. There are two more variations of binding operators, that bind much weaker and are discussed later.
Next, after the binding operators, is plain application. Juxtaposition of two terms means applying the first term to the second. Sequences of applications associate to the left. According to the vector notation convention the meaning of application depends on the type of the first term. Two forms of applications are defined by default: if the type of the first term is of arrow-form? then make-term-in-app-form is used; for the type of a free algebra we use the corresponding form of recursion. However, there is one exception: if the first term is of type boole application is read as a short-hand for the “if...then ...else” construct (which is a special form) rather than boolean recursion. The user may use the function add-new-application to add new forms of applications. This function takes two arguments, a predicate for the type of the first argument, and a function taking the two terms and returning another term intended to be the result of this form of application. Predicates are tested in the inverse order of their definition, so more general forms of applications should be added first.
By default these new forms of application are not used for output; but the user might declare that certain terms should be output as formal application. When doing so it is the user’s responisbility to make sure that the syntax used for the output can still be parsed correctly by the parser! To do so the function (add-new-application-syntax pred toarg toop) can be used, where the first argument has to be a predicate (i.e., a function mapping terms to #t and #f) telling whether this special form of application can be used. If so, the arguments toarg and toop have to be functions mapping the term to operator and argument of this “application” respectively.
After that, we have binary operators written in infix notation. In order of decreasing binding strength these are:
On the top level, we have two more forms of binding operators, one using the dot “.”, the other using square brackets “[ ]”. Recall that a binding operator is followed by a list of variables and a term. This notation can be augmented by a period “.” following after the variable list and before the term. In this case the scope of the binding extends as far to the right as possible. Bindings with the lambda operator can also be specified by including the list of variables in square brackets. In this case, again, the scope of the binding extends as far as possible.
Predefined operators are E and = as described above, the binding operator lambda, and the pairing operator @ with two prefix operators left and right for projection.
The value of an operator token is a function that will obtain the internal representation of the component terms as arguments and returns the internal representation of the whole term.
If a term is formed by application, the function make-gen-application is called with two subterms and returns the compound term. The default here (for terms with an arrow type) is to make a term in application form. However other rules of composition might be introduced easily.
Formulas are built from atomic formulas using junctors and quantors.
The simplest atomic formulas are made from terms using the implicit predicate “atom”. The semantics of this predicate is well defined only for terms of type boole. Further, a predicate constant (token type predconst) or a predicate variable (token type pvar) followed by a list of atomic terms is an atomic formula. Lastly, any formula enclosed in parentheses is considered an atomic formula.
The composition of formulas using junctors and quantors is very similar to the composition of terms using operators and binding. So, first postfix junctors, token type postfix-jct, are applied, next prefix junctors, token type prefix-jct, and quantors, token type quantor, in the usual form: quantor, list of variables, formula. Again, we have a notation using a period after the list of variables, making the scope of the quantor as large as possible. Predefined quantors are ex, excl, exca, and all.
The remaining junctors are binary junctors written in infix form. In order of decreasing binding strength we have:
Predefined junctors are & (and), ! (tensor), and -> (implication).
The value of junctors and quantors is a function that will be called with the appropriate subformulas, respectively variable lists, to produce the compound formula in internal form.