Das Gesetz der großen Zahlen

Der Physiker Marian von Smoluchowski (1872-1917) schrieb kurz vor seinem Tod den Artikel: ,,Über den Begriff des Zufalls und den Ursprung der Wahrscheinlichkeitsgesetze in der Physik.``( Smoluchowski 1918).Er stellte darin zwei Fragen:

1. Wie ist es möglich, daß sich der Effekt des Zufalls berechnen lasse, daß also zufällige Ursachen gesetzmäßige Wirkungen haben?
2. Wie kann der Zufall entstehen, wenn alles Geschehen nur auf regelmäßige Naturgesetze zurückzuführen ist? Oder mit anderen Worten: Wie können gesetzmäßige Ursachen eine zufällige Wirkung haben?

Auf die zweite Frage geht Smoluchowski nicht wirklich ein, und wir kommen nachher mit Boltzmann darauf zurück. Smoluchowski entwickelt die Antwort auf die erste Frage. Mit ,,gesetzmäßiger Wirkung`` meint er das Gesetz vom empirischen Mittel oder gleichbedeutend das Gesetz der großen Zahlen. Der ,,berechenbare Zufall`` offenbart sich in den voraussagbaren relativen Häufigkeiten oder allgemein in den empirischen Mitteln, die man mit den regellosen Versuchausgängen eines Experimentes bildet: Ein Münzwurfexperiment liefert bei 100-facher Wiederholung eine regellose Folge von Kopf und Zahl, wobei Kopf und Zahl ungefähr gleich häufig auftreten, die relative Häufigkeit von Kopf ist also ungefähr .

Smoluchowski untersucht die physikalischen Voraussetzungen, die eine solche regelmäßige Regellosigkeit ermöglichen. Diese liegen in der Instabilität der Bewegung, oder wie es Smoluchowski treffend auf den Punkt bringt: kleine Ursache, große Wirkung. Kleinste Schwankungen in den Anfangsdaten führen zu total verschiedenen Ausgängen. Der auf seine Spitze gestellte Bleistift ist ein einfaches Beispiel. Die kleinste Abweichung seines Schwerpunktes vom Lot bringt den Bleistift zu Fall. Zufällige Schwankungen in der Schwerpunktslage ergeben zufällige Richtungen, in die der Bleistift nach dem Fall zeigt. Man sollte sich wundern, daß diese Überlegung tatsächlich in die richtige Richtung weist, denn wie kann ,,Verstärkung`` des Zufalls durch Instabilität Gesetzmäßigkeit nach sich ziehen? Dabei darf man dann aber nicht vergessen, daß wir eine Gesetzmäßigkeit in der Regellosigkeit suchen.

Ein komplizierteres Beipiel ist das Galtonsche Brett (Galton (1822-1911)), bei welchem eine Kugel durch gegeneinander versetzte Nagelreihen fällt, wobei die Nagelabstände einer Reihe gerade etwas größer als der Kugeldurchmesser sind (siehe Abbildung 2 ). In jeder Nagelreihe trifft die Kugel zentral auf einen Nagelstift, wobei eine leichte zufällige Schwankung gegenüber der idealen zentralen Stoßlinie auftritt, die durch das Passieren der Kugel durch die vorherige Nagelreihe zustande kommt. Das Passieren der Kugel von zwei benachbarten Nagelstiften ist nämlich mit sehr, sehr vielen (inelastischen) Stößen zwischen der Kugel und den Stiften verbunden.

  
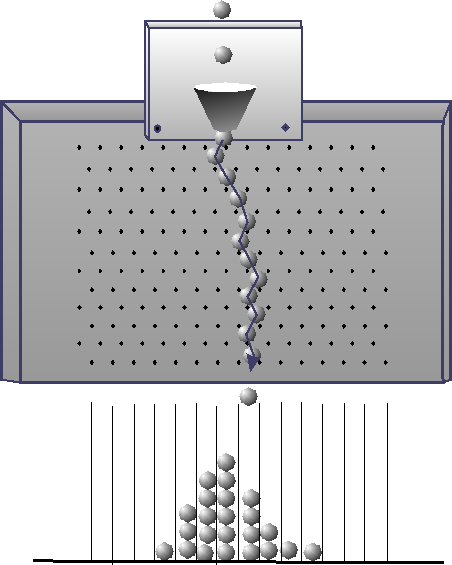
Abbildung 2: Das Galtonsche Brett

Diese haben zur Folge, daß selbst die kleinste Änderung der Eingangsrichtung, mit der die Kugel zwischen zwei Nagelstifte gerät, noch zum entgegengesetzten Ergebnis führen kann(wodurch die Details der Verteilung der Anfangsschwankung irrelevant werden): nämlich beim Auftreffen der Kugel auf den Nagelstift der nächst tieferliegenden Reihe nach rechts, statt nach links zu fallen. Eigentlich sind hierfür zwei Effekte verantwortlich, die in Abbildung 3 verdeutlicht sind. Dort verfolgen wir als Idealisierung statt der Kugel ein Punktteilchen, das zwischen zwei fetten runden Nagelstiften hin und her stoßend nach unten fällt. Wesentlich sind dabei nicht nur die vielen stattfindenden Stöße, sondern auch das von Stoß zu Stoß größer werdende Auseinanderklaffen von anfänglich nahe beieinanderliegenden Richtungen, was hier durch die Kreiskrümmung des Nagelstiftes zustande kommt (Abbildung 3 A). (Aus dem gleichen Grunde braucht man beim Billardspiel ein gutes Auge und eine ruhige Hand (vergleiche Ruelle 1992)).

Dieser Gedanke der starken Trennung von nahe beieinander liegenden Anfangsdaten durch die Dynamik im Laufe der Zeit (hier gerade die Zeit des Passierens zweier Stifte),wird heutzutage benutzt, um chaotisches Verhalten zu definieren. Smoluchowski beschreibt mit großer Sorgfalt diese Instabilität der Bewegung, die dazu führt, daß man letztlich aus der ungefähren Eingangsrichtung des Teilchens überhaupt nicht mehr auf die Ausgangsrichtung schließen kann. In jeder noch so kleinen Umgebung von Eingangsrichtungen gibt es Richtungen, die zu Ausgangsrichtungen ,,Links`` oder ,,Rechts`` führen. Und wenn die Eingangsrichtung noch genauer kontrolliert wird, so führt die (nun noch kleinere) Ungenauigkeit, die dieser besseren Kontrolle innewohnt, dennoch wieder zu völliger Unsicherheit über die Ausgangsrichtung.

  
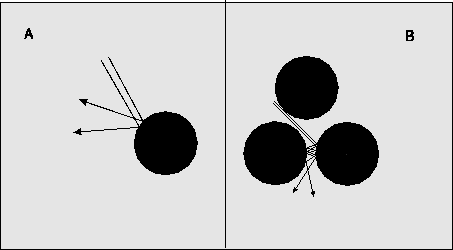
Abbildung 3: A: Zwei anfänglich nahe beieinander liegende Einfallsbahnen einer Punktmasse werden durch den Stoß mit der runden Nagelfläche aufgetrennt. B: Dieser Effekt wird durch die Anzahl von Stößen vergrößert. Je mehr Stöße stattfinden, desto kleiner kann die ,,Anfangsunsicherheit`` der Bahnen sein, so daß am Ende immer noch alle Ausgangsrichtungen herauskommen.

Im mathematischen Idealfall geht das so weiter ohne Ende. Hier ist ein mathematisches Beispiel dafür: Ich denke mir eine Zahl zwischen 0 und 1. Ich schreibe sie im Dualsystem auf. Ich schreibe eine sehr lange Zahl, bestehend aus Nullen und Einsen nach freiem Willen. Dann sage ich: ,,Die Zahl beginnt mit 0,0000``, und das sagt Ihnen, daß die Zahl zwischen 0 und liegt, aber mehr nicht. Sie können nicht sagen, was als nächste Ziffer folgt. Wenn ich Ihnen die sage, z.B. sei es eine 0, dann wissen Sie, daß die Zahl zwischen 0 und liegt, aber wie die nächste Ziffer aussieht, wissen Sie nicht. Und wenn es mir gelungen ist, eine ziemlich typische Zahl aufgeschrieben zu haben, die keine Regelmäßigkeit erkennen läßt, dann hilft Ihnen das genauere Eingrenzen der Zahl durch die Preisgabe einer weiteren Ziffer für das Festlegen der nächsten Ziffer überhaupt nicht.

Analog: Liegen zwei Eingangsrichtungen noch so nah beieinander, ist der Ausgang dennoch unbestimmt. Dieses ,,effektive Vergessen`` der jeweiligen Eingangsrichtung bei dem Passieren zweier Nagelstifte sorgt dafür, daß jede neue Rechts-Links-Entscheidung ,,unabhängig`` von der vorherigen wird, und diese Unabhängigkeit besteht so von Anfang an. Es ist die Anfangsunsicherheit beim ersten Auftreffen der Kugel im Galtonschen Brett, die ausreicht, um einen chaotischen Kugellauf zu produzieren.

Smoluchowski versucht also zu argumentieren, daß jede neue Links-Rechts-Entscheidung der Kugel unabhängig von der vorherigen wird, d.h. jede Links-Rechts-Entscheidung geschieht mit Wahrscheinlichkeit , ganz egal wie die vorherigen Entscheidungen ausfielen, womit sich eine einfache Wahrscheinlichkeitsvorhersage für den Endort der Kugel nach z.B. 12 Nagelreihen machen läßt: Die Wahrscheinlichkeit, daß die Kugel von ihrer Anfangsrichtung aus gesehen um 4 Plätze nach rechts verschoben ankommt, ist genauso groß, wie die Wahrscheinlichkeit, in einer Münzwurfreihe von 12 Würfen, 10 mal Kopf und 2 mal Zahl zu haben (= 0,016).

Aber was bedeuten hier diese Worte ,,Wahrscheinlichkeitsvorhersage`` und ,,Wahrscheinlichkeit``? Sie bedeuten, daß auf Grund eines statistischen Ansatzes oder, wie man auch sagt, einer statistischen Hypothese (über die gleich noch zu reden ist) und auf Grund der Instabilität des dynamischen Ablaufes eine experimentell überprüfbare Voraussage für relative Häufigkeiten in einem Galtonschen-Brett-Experiment möglich ist: Wenn nacheinander viele Kugeln das Brett durchlaufen (das nennt man ein statistisches Ensemble), wird sich typischerweise eine relative Häufung der Kugeln auf Endplätzen ergeben, die der berechneten relativen Häufigkeit, man sagt dann, der ,,Wahrscheinlichkeit``, gleicht: Von tausend Kugeln fallen ungefähr 16 auf Platz 4.

Diese Vorhersage heißt Gesetz der großen Zahlen, und die Berechnung der relativen Häufigkeiten geschieht mit Hilfe der Wahrscheinlichkeitstheorie. (Große Zahlen deshalb, weil erst viele Kugeln eine vernünftige relative Häufigkeit geben.) Die Instabilität der physikalischen Bewegung gestattet es, eine Voraussage über die relativen Häufigkeiten zu machen, wenn eine statistische Hypothese zugrunde gelegt wird. Die berechneten relativen Häufigkeiten nennt man Wahrscheinlichkeit.

Aber das ist nicht alles. Die schwierige zweite Frage, das eigentliche Problem, liegt noch vor uns, denn die statistische Hypothese ist noch unbegründet: Der erste kleine Zufall, der das erste Auftreffen der Kugel auf den ersten Nagelstift zufällig macht und der Zufall, der dafür sorgt, daß bei Wiederholung des Experimentes, beim Fallen einer neuen Kugel, die ,,Karten neu gemischt`` sind--woher kommt dieser Zufall? Offenbar gibt es ja Anfangsbedingungen, bei denen die Kugel auch auf Platz 4 fällt-- warum fällt nicht jede Kugel auf Platz 4? Warum sind bei jeder Wiederholung des Experimentes die Karten neu gemischt? Was beschreibt diesen ,,äußeren`` Zufall? Diese nicht näher beschriebene statistische Hypothese wird üblicherweise wieder eine Hypothese über ein tatsächliches Ensemble sein: Wir können darauf verweisen, daß die Maschine, die die Kugeln auf den Weg schickt, von Mal zu Mal Störungen durch die Umgebung ausgesetzt ist, die dafür sorgen, daß ein statistisches Ensemble an Anfangssituationen vorliegt, so daß sich typischerweise das beobachtete, zufällige Verhalten ergibt (siehe Abbildung 4 ).

  
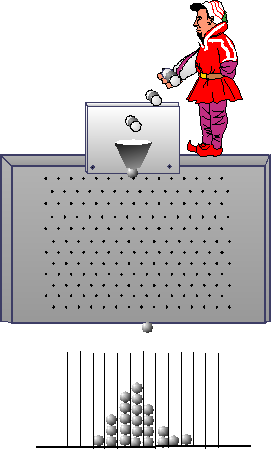
Abbildung 4: Das Hereinfallen der Kugeln ist mit Zufall behaftet: Der äußere Zufall!

(Bei genügender Isolation und Präzisionsarbeit des Brettes und der Einwurfmaschine sollte dann der Zufall gänzlich verschwinden.) Aber damit haben wir die Wurzel des Zufalls nur weiter verschoben zu einem neuen äußeren Zufall in einer größeren Umgebung des Geschehens, der die Störung reguliert. Und solange jedes System Teil eines größeren Systems ist, wird diese Verschiebung des Zufalls passieren. Dies ist aber weder als unbefriedigend noch beunruhigend anzusehen, vielmehr führt es direkt zur Antwort auf die zweite Frage.

Ich will jetzt aber erst noch kurz erwähnen, daß der Physiker Willard Gibbs
(1844-1906) eine Art axiomatischen Aufbau der sogenannten Statistischen Mechanik schuf, indem er einfach die letztendliche Begründung der statistischen Hypothese, die Boltzmann beschäftigte, verdrängte. In seiner Arbeit formulierte er einen ,,allgemeingültigen Ansatz für statistische Hypothesen`` über das typische Verhalten komplexer Systeme (z.B. Systeme mit vielen Teilchen), worin nur das zu Grunde liegende physikalische Gesetz eingeht. Der Gibbssche Formalismus entsprach in seiner ,,Anwendbarkeit`` sehr dem Geschmack der Physiker und wurde seitdem mit großem Erfolg, insbesondere eben in der Statistischen Mechanik, angewandt. Gleichzeitig aber war die Gibbssche Grundidee schwierig, denn das Gibbssche Ensemble ist eigentlich ein rein gedankliches (eine gedankliche Ansammlung von gleichen Systemen mit einer gewissen relativen Häufigkeitsverteilung)--in unserer modernen Sprache einfach ein Wahrscheinlichkeitsmaß-- eben nur eines, um ,,typisch`` zu definieren. In diesem Sinne ist die Gibbssche Idee identisch mit der von Boltzmann.

Die Basis für den Gibbsschen Ansatz war der Begriff des thermischen Gleichgewichtes, eines makroskopisch zeitlich nicht veränderlichen Verhaltens, aber wir brauchen dies nicht weiter auszuführen, weil die Idee gleich etwas allgemeiner besprochen wird.