Die Antwort auf die Frage: "Was ist Geometrie?"
ist ziemlich klar. Es ist die Lehre von der
räumlichen Ausdehnung, und ihre Elemente sind
anschauliche Begriffe wie Punkt und Gerade. Die
Antwort auf die Frage: "Was ist Analysis?"
fällt heute ebenso leicht, obwohl die
Anschaulichkeit einer begreifbaren Abstraktion
weichen muß. Es ist die Lehre vom Grenzprozess,
vom Argumentieren mit Unendlich. Ihre Elemente sind
das Kontinuum-der Zahlenstrahl ohne Lücken-und
die reellen Zahlen. Was ist eine reelle Zahl? Eine
relle Zahl zwischen 0 und 1 ist eine unendliche
Folge bestehend aus den Ziffern 0,1,2,...,9 etwa
0,0564319.... Im Zweiersystem oder Dualsystem,
wie man auch sagt, benutzt man nur die Ziffern
0,1, so daß jede Zahl zwischen 0 und 1 eine
01-Folge ist: ![]() .
.
Was aber ist Wahrscheinlichkeitstheorie? Sagt man: "Die Lehre vom Zufall", so benutzt man nur ein anderes Wort für Wahrscheinlichkeit. Was ist Zufall? Wir können an Vorhersage denken, und den Zufall mit dem Unvorhersagbaren in Verbindung bringen. Das entspricht dem alltäglichen Gefühl und wird damit vielleicht begrifflich klarer. Aber dann gibt es weitere Fragen: Wie kann es eine Lehre vom Unvorhersagbaren geben? Ist das nicht geradezu widersprüchlich? Und ist das Unvorhersagbare nur aus Unkenntnis, aus Ignoranz unvorhersagbar oder ist da etwas Prinzipielles, nicht Wissenbares im Spiel?
Die mathematisch formulierten physikalischen Gesetze geben eine vorausberechenbare, d.h. eine determinierte Entwicklung der Welt, wenn die Anfangsdaten bekannt sind. Dies ist eine Tatsache, die Poincaré(1854-1912) in Bezug auf Wahrscheinlichkeit so formulierte: "Wenn wir nicht unwissend wären, gäbe es keine Wahrscheinlichkeit"(Poincaré; 1914). Dabei sollte es zunächst gleichgültig sein, ob unser Unwissen prinzipieller Natur ist oder ob unsere Ignoranz nur eine vordergründige, auf Bequemlichkeit beruhende ist.
Es wäre aber falsch, Poincarés Aussage zu eng zu nehmen und Wahrscheinlichkeit vollkommen an Unwissen zu heften, denn Wissen und Unwissen sind viel zu komplizierte Begriffe und nur schwer zu objektivieren. Dabei geht es ja bei der Benutzung von Wahrscheinlichkeiten letztlich um die Beschreibung eines objektiven Sachverhaltes, wie dem Ablauf eines physikalischen Systems, der natürlich völlig unabhängig davon ist, wieviel wir von ihm wissen oder bei seiner Beschreibung von unserem Wissen preisgeben wollen.
Darum ist unsere Sichtweise der Wahrscheinlichkeitsbeschreibung eines physikalischen Geschehens eine praktische und durchaus vereinbar mit der Vorstellung, daß es uns zwar möglich wäre, wir es aber einfach als unpraktisch empfinden, eine detaillierte Berechnung des Ablaufes aus den physikalischen Gesetzen vorzunehmen.
Was also ist dann Wahrscheinlichkeitstheorie? Es
ist die Lehre vom typischen Verhalten (von
physikalischen Systemen). Der Begriff des
Typischen ist als mathematischer Begriff sicher
ungewöhnlicher als der der räumlichen Ausdehnung
oder der des Grenzprozesses, aber er ist ebenfalls
hinreichend offenbar, gleich verstanden zu werden.
Typischerweise ist ein Los eine Niete,
typischerweise zeigt eine Münzwurfreihe
unregelmäßige Ausgänge, mit ungefähr ![]() Anteil an Kopf und
Anteil an Kopf und ![]() Anteil an Zahl.
Typischerweise kommt in einer langen Münzwurfreihe
irgendwann einmal 6 mal Kopf in Serie. In einer
Münzwurfreihe von 100 Würfen ist es untypisch,
50 mal Kopf hintereinander zu haben.
Anteil an Zahl.
Typischerweise kommt in einer langen Münzwurfreihe
irgendwann einmal 6 mal Kopf in Serie. In einer
Münzwurfreihe von 100 Würfen ist es untypisch,
50 mal Kopf hintereinander zu haben.
Die mathematischen Größen, auf denen Wahrscheinlichkeitstheorie aufbaut, sind die physikalischen Variablen, die Anfangswerte, die zusammen mit den physikalischen Gesetzen den physikalischen Ablauf eines Systems festlegen. Als ein klassisches Beispiel denken wir an ein Gas in einem Volumen, das wir in diesem Moment (den wir den Anfangszeitpunkt t=0 nennen) betrachten. Die einzelnen Gasteilchen gehorchen (sagen wir) der Newtonschen Mechanik. Dann bestimmen die momentanen Orte und Geschwindigkeiten der Gasteilchen die weitere (und die vergangene) zeitliche Entwicklung des Gassystems vollkommen, solange jedenfalls, als kein Eingriff von außen erfolgt.
Der momentane Zustand des Gassytems sei nun so, daß die Teilchen das Volumen ziemlich homogen ausfüllen. In der uns eigenen makroskopischen Sichtweise des Gases sehen wir nicht die einzelnen Gasmoleküle, sondern erfahren nur die homogene Dichteverteilung des Gases im Volumen, wir nennen das einen Makrozustand. Der detaillierte mikroskopische Zustand des Gases, bei dem die einzelnen Teilchen durch ihre Orte und Geschwindigkeiten beschrieben werden, heißt entsprechend Mikrozustand. Offenbar ändern sich die Mikrozustände andauernd, denn die Orte und Geschwindigkeiten der Gasteilchen verändern sich mit der Zeit. Aber das merken wir am Makrozustand nicht. Dafür sind unsere Empfindungen viel zu grob ausgelegt. Wenn nun ein solcher homogener Makrozustand vorliegt, können wir sicher sein, daß er sich im Laufe der Zeit nicht verändern wird. Warum? Weil die Anzahl der Möglichkeiten, das ist die Anzahl der Orte und Geschwindigkeiten (also der Anfangsbedingungen) der Gasmoleküle (der momentanen Mikrozustände), die zu einer zeitlichen Entwicklung führen, die das makroskopische Bild nicht verändern, unglaublich ungeheuer viel größer ist, als die Anzahl der Möglichkeiten, die zu einem anderen Makrozustand führen: Z. B. zu einem, bei dem das Volumen zur Hälfte gasleer ist (siehe Abbildung 1). Typischerweise wird das Gas den Raum homogen ausfüllen, das bedeutet, bei den weitaus allermeisten Möglichkeiten von Anfangsbedingungen füllt das Gas das Volumen homogen aus.
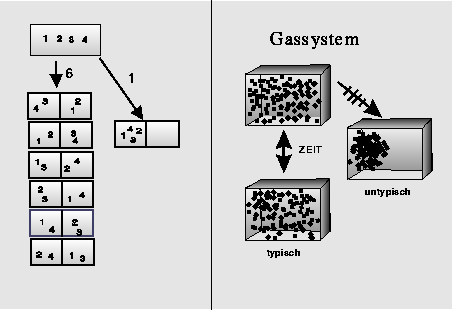
Abbildung 1: Es gibt 6 Möglichkeiten, 4 Objekte auf
zwei Behälter zu verteilen, so daß in jedem
Behälter 2 Objekte sind. Es gibt nur 1
Möglichkeit einer 4-0-Aufteilung. Der
Unterschied zwischen der Anzahl der
Möglichkeiten für Gleichverteilung und für
deutlich ungleiche Aufteilungen (wie bei dem
Gassystem auf der rechten Seite), steigt
astronomisch schnell mit der Anzahl der Objekte.
Dieses Argument verdanken wir dem Physiker Ludwig Boltzmann (1844-1906), der die kinetische Gastheorie von Clausius (1822-1888) und Maxwell (1831-1879) zu ihrer Vollendung führte. Boltzmann formulierte klar und deutlich die Einsicht, daß ein physikalisches Geschehen unter den gegebenen Bedingungen typisch ist, d.h. daß der Ablauf immer so ist, wie die allermeisten Abläufe geschehen. (Daß ich hier "unter den gegebenen Bedingungen" sage, hat einen Grund, über den ich nachher rede.)
Die Boltzmannsche Einsicht, die ich im folgenden weiter ausführen werde, ist eine der Physik übergeordnete, unabhängig von der speziellen Form der physikalischen Gesetze, und es ist deshalb gleichgültig, aus welchem Bereich der Physik wir die Beispiele nehmen. Der besseren Anschauung halber betrachten wir zuerst nur die gewohnte Newtonsche Mechanik.
Statt "typisch" habe ich oben von den "weitaus allermeisten" Möglichkeiten gesprochen, aber ich muß sagen, was das mathematisch sein soll, wenn die Orte und Geschwindigkeiten stetig variieren und es unendlich viele Möglichkeiten für das eine wie für das andere gibt, wenn also im eigentlichen Sinne nicht mehr von Anzahl gesprochen werden kann. Hierfür wurde die Wahrscheinlichkeitstheorie entdeckt, die einen natürlichen Inhaltsbegriff von Mengen benutzt, genannt Wahrscheinlichkeitsmaß oder einfach nur Wahrscheinlichkeit, wozu nachher noch etwas gesagt wird.
Aber noch wichtiger als die mathematische Erklärung dieser Wörter ist die Einsicht, daß hier etwas Objektives über die Physik von Systemen gesagt wird: Was das physikalische System offenbart, ist typisch! Es ist das, was es in den allermeisten Fällen, das bedeutet für die allermeisten Anfangsbedingungen, offenbart. Dadurch können wir Voraussagen auch für sehr komplexe Systeme machen, ohne daß wir detaillierte Teilchenbahnen berechnen müssen. Und das genau ist die Rolle des Zufalls in der Physik.