Wir kommen zur Boltzmannschen Einsicht. Man muß bereit sein zu erkennen, daß jede statistische Hypothese auf einem äußeren Zufall beruht; der eine Zufall, den man gerade beschrieben hat, hat seine Wurzel in einem noch unergründeten Zufall eines umfassenderen Systems, und wenn man den Zufall dann beschrieben hat, dann nur unter Benutzung des Zufalls eines noch umfassenderen Systems. Und dies geht so weiter und weiter, denn jedes System ist Teil eines größeren, und jedes System hat Kontakt mit jedem größeren; auch wenn man es schafft, ein System kurzzeitig zu isolieren, so war es vorher in Kontakt mit seiner Umgebung, und so geht das ohne Ende. Ohne Ende? Falsch! Es muß aufhören beim größten möglichen System, das alle anderen Systeme enthält, beim Universum nämlich. Das Universum gibt es nur einmal, es ist wie es ist, hier können keine Karten neu gemischt werden, hier müssen wir die zweite Frage beantworten. Die Antwort ist zwangsläufig: Von allen möglichen Universen erleben wir unter den gegebenen Bedingungen ein typisches, wir erleben das, was die allermeisten Universen offenbaren würden. Was zu beweisen wäre: Die meisten Universen offenbaren in statistischen Ensemblen von ihren (lächerlich) kleinen Teilsystemen relative Häufigkeiten, die z.B. der statistischen Hypothese von Smoluchowski oder von Gibbs entsprechen.
Vielen Physikern ist das Universum viel zu groß, um solche Aussagen ernst zu nehmen, denn was kann nicht alles passieren, vor allem kennen wir die Physik des Universums noch gar nicht. Das ist richtig, aber unwesentlich für das Verständnis des Problems: Die prinzipielle Frage ändert sich nämlich nicht mit neuen physikalischen Theorien, die die alten ablösen und erklären, das sah Boltzmann deutlich und scheute sich nicht, über das Universum zu reden--auch wenn sich nichts beweisen ließ.
Wie definiert man ein typisches Universum? Was gilt
für die allermeisten Zahlen zwischen 0 und 1?
Typischerweise gilt, daß in der Dualdarstellung
die Ziffern 0 und 1 mit relativer Häufigkeit
jeweils 
auftreten. Dies ist ein
mathematisches Münzwurfmodell! Die Menge der
Zahlen mit dieser Eigenschaft ist also eine große
Menge. Sie enthält die allermeisten Zahlen
zwischen 0 und 1. Zahlen, die nicht dazu
gehören, sind z. B.:
also 0,1000...; 0,01000...;0,001000.... Diese
unendlich vielen Zahlen sind im Vergleich zu den
anderen verschwindend wenige. Sie bilden eine
Menge, deren Größe nichts ist im
Vergleich. Der Begriff der Größe der Menge
ist hier einfach der des Rauminhaltes, das
Volumen, das die Zahlen einnehmen. Das Volumen
des Intervalls [a,b] auf dem Zahlenstrahl ist
b-a, das aller Zahlen zwischen 0 und 1 ist
also 1. Wenn man aus diesem Intervall alle Zahlen
der Form 
entfernt, dann ist das
Volumen immer noch 1.
Entscheidend also ist das Volumen, oder wie man in der Wahrscheinlichkeitstheorie sagt, das Maß einer Menge. Eine Eigenschaft gilt typischerweise, wenn das Maß der Menge aller Zahlen mit dieser Eigenschaft ungefähr 1 ist. Das Volumenmaß auf der Zahlenmenge ist von dem französischen Mathematiker Lebesgue (1875-1941) eingeführt worden, den der russische Mathematiker Kolmogoroff (1903-1987) dann für die Wahrscheinlichkeitstheorie übernommen hat. Unser Zahlenbeispiel ist ein rein mathematisches, und da ist das Maß für Typisches 1 und für Untypisches 0. In der Physik ist das Maß nahe bei 1 oder einfach sehr groß oder nahe bei 0 oder einfach sehr klein.
Also, wie definiert man ein typisches Universum?
Zur Zeit Boltzmanns war das Bild, das man sich vom
Universum machte, mechanistisch, d.h. bestehend aus
enorm vielen Teilchen, die der Newtonschen Mechanik
gehorchen. Also ein riesiges Gassystem. Der Ablauf
des Universums ist durch die anfänglichen Orte
(die üblicherweise mit q bezeichnet werden) und
Geschwindigkeiten (die üblicherweise mit v
bezeichnet werden) aller Teilchen festgelegt.
Verschiedene Anfangsbedingungen liefern
verschiedene Universen. Die Menge aller Universen
ist gleichbedeutend mit der Menge aller
Anfangsbedingungen für die Orte und
Geschwindigkeiten. Bei dieser Vorstellung gelangen
wir zu einer Abstraktionsstufe, die seit der Zeit
Boltzmanns immer wieder zu Verwirrung führte. Die
Menge aller Anfangsbedingungen nannte Boltzmann
Phasenraum. Die Phase ist die Größe, die die
zeitliche Entwicklung eines Systems determiniert,
also in der Newtonschen Mechanik die Gesamtheit
aller Orte und Geschwindigkeiten der Teilchen des
Systems.
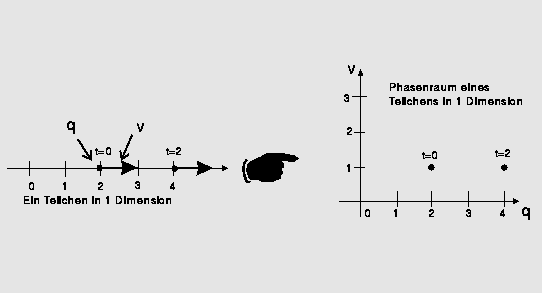
Abbildung 5: Der Phasenraum für ein Teilchen in
einem eindimensionalen Raum ist
zweidimensional.Im gezeigten Bild bewegt sich das
Teilchen in zwei Zeiteinheiten nach rechts mit
Geschwindigkeit 1.
Der sogenannte physikalische Raum, d. h. der Raum
unserer Anschauung, ist 3-dimensional, es gibt
drei aufeinander senkrecht stehende Achsen, auf
denen man die Koordinaten eines Teilchens abträgt,
und die Angabe dieser Koordinaten legt den Ort des
Teilchens im Raum fest. Das ist anschaulich. Im
Phasenraum eines Systems von N Teilchen haben wir
aber 3N+3N=6N Achsen, für jedes Teilchen 3
Achsen, auf denen man die Ortskoordinaten des
betreffenden Teilchens abträgt, und nochmal 3
Achsen, auf denen man die
Geschwindigkeitskoordinaten abträgt, weil die
Geschwindigkeit eines jeden Teilchens auch
3-dimensional ist. Der Phasenraum ist also
6N-dimensional (eine typische Zahl für ein
kleines Gassystem ist 
). Der Begriff des
Phasenraums verlangt also schon einiges an
Abstraktionsvermögen (siehe Abbildung 5).
An Stelle des Intervalls [0,1] tritt nun der Phasenraum des Universums, und jeder Punkt im Phasenraum ist ein Universum. Um vom typischen Universum reden zu können, muß ein Inhalt, ein Volumen auf dem Phasenraum, eingeführt werden. Was für ein Volumenmaß sollte man nehmen? Irgendeines? Das wäre lächerlich. Das Maß muß eines sein, das vom physikalischen Gesetz selbst bestimmt wird. Aber was soll das heißen? Man kann das auf verschiedene Arten sagen: Die Bedeutung von ,,typisch`` muß zeitlos sein. Anders ausgedrückt: Wir haben von ,,Anfangsdaten`` gesprochen, aber das Wort ,,Anfang`` ist nicht ernst zu nehmen, der Anfang ist ja nur ein willkürlicher Zeitpunkt, ein Zeitpunkt, zu dem definiert wird, was ,,typisch`` bedeuten soll. Das muß zu jeder Zeit möglich sein: Ein typischer Phasenraumpunkt bleibt unter der Zeitentwicklung typisch.(Daß in einem Modell des Universums ein ,,Urknall`` den Beginn des Universums definiert, ist für diese Überlegung zunächst uninteressant.)
Dies bedeutet, daß das physikalisch richtige
Volumenmaß zeitlich unveränderlich sein
muß, und das wiederum bedeutet folgendes: Man
wähle zur Zeit 0 eine Menge M im Phasenraum
aus (siehe Abbildung 6), diese Menge besteht aus
Punkten x in M, und jeder Punkt steht für ein
Universum, dessen zeitliche Entwicklung durch den
Phasenraumpunkt x festgelegt ist. Zu einer
späteren Zeit haben die Orte und Geschwindigkeiten
der Teilchen des Universums andere Werte, die
Teilchen bewegen sich ja nach den Newtonschen
Gesetzen, d.h. dem zeitlich veränderten Universum
entspricht ein neuer Punkt x(t) im Phasenraum.
Die zeitliche Entwicklung eines Universums gibt
demnach im Phasenraum eine Kurve von x nach
x(t), und verfolgt man alle Punkte der Menge M,
so haben wir viele Kurven. Zwei Kurven können sich
übrigens nie durchkreuzen. Man nennt die
Gesamtheit aller solcher Kurven im Phasenraum einen
Fluß. Die Punkte der Menge M wandern also
im Laufe der Zeit im Phasenraum umher, und zur Zeit
t bilden die Punkte x(t) die Menge M(t). Ein
zeitunabhängiges Maß--man sagt auch
stationäres Maß--ist dann ein Maß, das jeder
solchen Menge M(t) den gleichen Inhalt wie der
ursprünglichen Menge M zuordnet:
für alle t.
Haben wir ein solches Maß gefunden (und das ist
eine mathematische Aufgabe), können wir damit
,,typisch`` definieren.
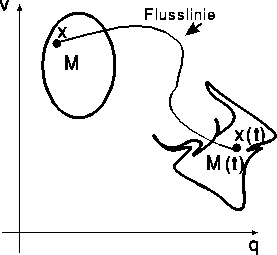
Abbildung 6: Unter dem Fluß auf dem Phasenraum wird eine Punktmenge verändert.
Gesucht ist ein Maß, das jeder
Menge M und der aus ihr enstandenen Menge M(t)
die gleiche Größe zuordnet.
Das sieht nun alles hoffnungslos kompliziert aus. Um das stationäre Maß zu finden, muß man den Fluß auf dem Phasenraum kennen, d.h. wir müssen die Newtonsche Mechanik unseres 3-dimensionalen Raumes nun zu einer Dynamik auf den Phasenraum passend umformulieren. Aber das war zur Zeit Boltzmanns längst geschehen! Die Lagrangesche Formulierung der Mechanik und die ganz analoge Hamiltonsche Mechanik, nach ihrem Entdecker, dem mathematischen Physiker Hamilton (1805-1865), benannt, ist eine Formulierung der Newtonschen Mechanik auf dem Phasenraum. Und selbst das stationäre Maß war bekannt. Der Mathematiker Liouville (1809-1882)hatte bewiesen (mit einem ganz einfachen Argument), daß der gewöhnliche Rauminhalt (nur auf entsprechend hohe Dimension verallgemeinert)sich unter dem Hamiltonschen Fluß nicht verändert. Damit ist man schon am Ziel. Wir wissen jetzt wie man ,,typisch`` zu definieren hat, mit dem anschaulichen Volumenmaß, ganz analog wie beim Zahlenstrahl. Übrigens, unser kombinatorisches Argument oben, wonach die Anzahl der Möglichkeiten der Gleichverteilung am weitaus größten ist (siehe Abbildung 1), stellt im wesentlichen eine Berechnung dieses Phasenraumvolumens dar, das zu einem Makrozustand homogener Dichte gehört.
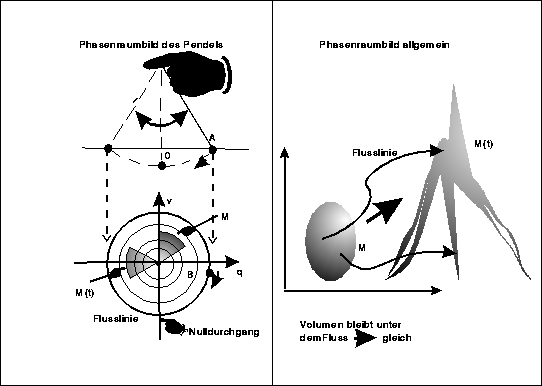
Abbildung 7: Phasenraumbilder: Links ein Pendel mit Ausschlag
(Amplitude) A und Schwingungsfrequenz 1. Wäre die
Amplitude B (kleiner als A), so wäre die
zugehörige Phasenraumkurve der kleinere Kreis
B.Gemäß dem Liouvilleschen Satz verändert sich
beim klassischen Fluss im Phasenraum der
Rauminhalt einer Menge nicht. Dies ist beim
Pendel leicht zu sehen, indem man ein
,,Tortenstück`` verfolgt.Im allgemeinen aber
(rechtes Bild), z.B. für ein Gas in einem
Volumen, wird aus einer schönen Menge von
Phasenraumpunkten ein stark zerfasertes
Geflecht.
Und so hat Gibbs seine statistische Hypothese formuliert: Er hat einfach jedes genügend isolierte System wie ein Universum behandelt und ,,typisch`` gemäß dem zugehörigen stationären Maß definiert, welches durch das das System beschreibende physikalische Gesetz bestimmt wird.
Nun muß man ,,nur noch`` zeigen, daß in typischen Universen sich bei den (lächerlich kleinen) Teilsystemen, wie dem unwürdigen Glücksspiel auf irgendeiner Straße, die relativen Häufigkeiten so ergeben, wie sie es tun, d.h. daß die Gibbsche Hypothese typischerweise korrekt ist. Hätte man jemals gedacht, daß die Kugeln im Galtonschen Brett einer universalen Eingebung folgen? Aber das folgt tatsächlich aus der Physik. Mancheiner wird jetzt dabei im Hinblick auf unsere Welt ein ungutes Gefühl haben, die erscheint ihm doch ganz anders--insgesamt untypisch. Denn wendet man nicht fortwährend Physik ohne Zufall an? Wir heben einen Apfel auf und lassen ihn fallen und können dessen Fall berechnen, präzise und ohne Zufall.
Was man zeigen sollte, ist nie gezeigt worden. Jedenfalls nicht für das Newtonsche Universum. Wen wundert das nicht? Aber es ist nicht gezeigt worden, weil es etwa zu schwer wäre. Nein, es ist nicht gezeigt worden, weil unser Universum untypisch ist. Für uns ist es typisch, untypische Situationen herzustellen (wir können alle Gasmoleküle in einem Volumen durch einen Kolben in einer Hälfte des Volumens zusammendrücken, und dann den Kolben schnell entfernen, so daß die untypische Situation in Abbildung 1 vorliegt), wir können uns sogar vorstellen, daß wir in der Lage sind, den Zufall durch präziseste Kontrolle auszuschließen. Offenbar ist die Gibbsche Hypothese oft falsch und nur manchmal richtig. Dadurch sind wir, und das zurecht, vollkommen verunsichert, wann denn nun typisches Verhalten--Gleichgewichtsverhalten--vorliegt und wann nicht. Darüber kann natürlich nicht hinweggegangen werden, und ich werde, bevor ich über Boltzmanns endgültigen Sieg in der Quantenmechanik spreche, dazu kurz etwas sagen.