Department Mathematik
print
Navigationspfad
Inhaltsbereich

Zetafunktion und Riemannsche Vermutung

Vorlesung von O. Forster im WS 2017/18
am Mathematischen Institut der LMU München

Mi, Fr 14-16, HS A027, Theresienstr. 39
mit 2std. Übungen Mi 16-18 (A027)

Beschreibung

Für s > 1 konvergiert die unendliche Reihe
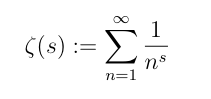
  zeta(s) = \sum {1/n^s: n >= 1}
Schon Euler befasste sich mit dieser Reihe und stellte einen Zusammenhang mit der Primzahl-Verteilung her. Ihre wahre Bedeutung erhielt diese Funktion erst durch B. Riemann mit seiner 1859 erschienenen Arbeit
     "Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse".
Darin betrachtete Riemann die Zetafunktion als Funktion einer komplexen Variablen s und bewies, dass sich diese Funktion in die ganze komplexe Zahlen-Ebene mit Ausnahme des Punktes s=1 holomorph fortsetzen lässt. Bei s=1 hat die Funktion einen Pol erster Ordnung. Riemann bewies die sog. Funktionalgleichung der Zetafunktion, das ist eine gewisse Symmetrie-Eigenschaft bzgl. des Punktes s = 1/2, und gab explizite Formeln an, welche die Funktion pi(x), die die Primzahlen <= x zählt, mit den nicht-reellen Nullstellen der Zetafunktion verbinden. Dabei stellte er die Vermutung auf, dass diese sog. nicht-trivialen Nullstellen alle den Realteil 1/2 haben und schreibt dazu: "Hierfür wäre allerdings ein strenger Beweis zu wünschen; ich habe indess die Aufsuchung desselben nach einigen flüchtigen vergeblichen Versuchen vorläufig bei Seite gelassen ...". Bis heute ist diese Vermutung unbewiesen. Sie zählt zu den mit einer Million Dollar dotierten Millennium-Problemen des Clay Mathematics Institute.
In der Vorlesung stellen wir die Zetafunktion und ihre wichtigsten Eigenschaften vor. Aus der Tatsache, dass zeta(s) keine Nullstellen mit Re(s) = 1 hat, folgt der zuerst von Hadamard und de la Vallee Poussin 1896 bewiesene Primzahlsatz. Dieser besagt, dass pi(x) für x gegen unendlich asymptotisch gleich dem Integral-Logarithmus Li(x) ist. Li(x) ist das Integral über 1/log(t) von t=2 bis x. Die Riemannschen Vermutung ist äquivalent zur Aussage, dass die Differenz pi(x) - Li(x) die Größenordnung O(sqrt(x)log(x)) hat. Wir beweisen außerdem einige weitere Äquivalenzen zur Riemannschen Vermutung.

Vorkenntnisse:
Funktionentheorie; Vorlesung Algebra und/oder Zahlentheorie

Für
Master-Studenten der Mathematik und andere Interessierte mit entsprechenden Vorkenntnissen

Gliederung
(Zu einigen Kapiteln gibt es ein Skriptum)

  1. Zetafunktion und Euler-Produkt
  2. Die Euler-Maclaurinsche Summations-Formel
  3. Allgemeine Sätze über Dirichlet-Reihen
  4. Beweis des Primzahl-Satzes    (pdf)
  5. Funktional-Gleichung der Zetafunktion    (pdf)
    Anhang: Die Gamma-Funktion    (pdf)
  6. Nullstellen-Verteilung im kritischen Streifen    (pdf)
  7. Die Mellin-Transformation und ihre Umkehrung    (pdf)
  8. Äquivalenzen zur Riemannschen Vermutung    (pdf)

Literatur

  • P.Borwein / S.Choi / B.Rooney / A.Weirathmueller (eds.): The Riemann Hypothesis. CMS Books in Math. Springer 2008
  • J. Brüdern: Einführung in die analytische Zahlentheorie. Springer 1995
  • H.M. Edwards: Riemann's Zeta Function. Academic Press 1974. Nachdruck Dover 2001
  • E. Landau: Vorlesungen über Zahlentheorie, Vol. II, Hirzel 1927. Nachdruck Chelsea 1969.
  • S.J. Patterson: An introduction to the theory of the Riemann Zeta-Function. Cambridge UP 1988
  • K. Prachar: Primzahlverteilung. Springer 1957
  • G. Tenenbaum: Introduction to Analytic and Probabilistic Number Theory. AMS, 3rd ed. 2015
  • E.C. Titchmarsh: The Theory of the Riemann Zeta-Function. Oxford UP, 2nd ed. 1986

Vorlesungen vergangener Semester

Bücher/Books    Eprints    Software
Otto Forster 2017-10-15