Anhang: Das Galileische Fallgesetz

Den Gedankengang habe ich von Reinhard Lang [2].

Das Fallgesetz besagt, daß alle Massen im Vakuum mit der gleichen Beschleunigung g fallen. Der Fallweg in der Zeit t ist dann, wenn bei null startend,

Die Frage ist: Wie kommt man darauf? Wie akm Galilei darauf? Antwort: Durch Nachdenken. Aus einem Gedankenexperiment folgert man, daß alle Körper gleich schnell fallen, und daß die Geschwindigkeit proportional zur Zeit ist.

1. Alle Körper fallen gleich schnell. Angenommen die Geschwindigkeit eines schwereren Körpers sei größer als die eines leichteren. Also die eines Steines sei größer als die eines leichteren Stück Holzes :
   
   Dann verbinde beide Körper mit einem Faden und man bekommt
   
   weil beide zusammen schwerer als der Stein sind, aber auch
   
   weil Holz ja den Stein bremst. Also ergibt sich ein Widerspruch. Also fallen alle Körper gleich schnell.
2. Wie lautet die Geschwindigkeit als Funktion der Zeit?

   Annahmen: Man könnte denken, am einfachsten ist: , denn der Weg ist ja die naturlichste Größe. Das geht aber nicht, denn die Lösung davon wäre die Expontialfunktion für , was unsinnig ist, denn der Körper fällt, ganz egal ob man den Anfangsort als null ansieht oder nicht.

   Dann versucht man , also v=gt, mit g als Proportionalitätskonstante. Daraus gewinnt man s, denn und das Aufsummieren gibt die Fläche (Abbildung 1) unter dem Dreieck: Dieser Zusammenhang wird später der fundamentale Satz der Analysis.

    
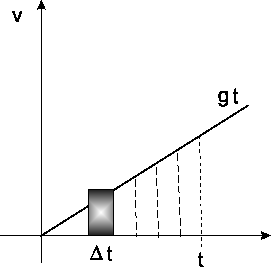
   Abbildung: Das Geschwindigkeits-Zeit Diagramm. Der Weg bis zur Zeit t ist die Summe aller infinitesimalen Rechtecksflächen, die die Dreiecksfläche unter dem Geradenstück ergeben 
   

   Man sagt, daß Galilei dies dann anschließend experimentel überprüft hat. Oder hat er nicht vielmehr den Erdanziehungsfaktor g bestimmt? Denn der ist ja real, auf Grund des vorher gedachten Fallgesetzes.