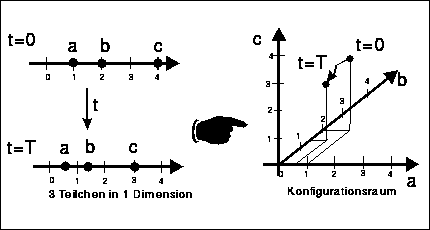
Abbildung 9: Der Wanderung von 3 Teilchen im physikalischen Raum (hier in einer Dimension) entspricht im 3-dimensionalen Konfigurationsraum eine Bahn
Boltzmanns Idee der Begründung der statistischen Hypothese und der Gibbssche statistische Ansatz sind unabhängig von der speziellen Gestalt zugrunde liegenden der physikalischen Theorie. Es ist eigentlich gleichgültig, ob die Welt aus Punkt-Teilchen besteht, aus Feldern oder aus Fäden-Teilchen (Strings) oder wer weiß sonst was. Solange es für diese Größen physikalische Gesetze gibt, steht der Boltzmannschen Einsicht der typischen Bewegung nichts entgegen. Man kann natürlich durch das Problem der Irreversibilität abgeschreckt sein, aber das sollte man nicht. Man sollte sich nur dieses Problems bewußt sein.

Abbildung 9: Der Wanderung von 3 Teilchen im
physikalischen Raum (hier in einer Dimension)
entspricht im 3-dimensionalen Konfigurationsraum
eine Bahn
Die Newtonsche Mechanik wird ja von der Quantenmechanik abgelöst, was bedeutet, daß die Quantenmechanik allgemeingültiger als die Newtonsche Mechanik ist und diese zu erklären hat (siehe z. B. Weinberg 1997). Diese Sicht der Quantenmechanik wird noch nicht von allen Physikern geteilt, insbesondere war dies nicht die Sicht von Niels Bohr, einem der Begründer der Quantenmechanik. Aber wenn man einmal diese Sicht hat, dann muß sich die Bewegung der Punkt-Teilchen der Newtonschen Mechanik aus der Quantenmechanik ergeben. Die bisherige Lehrbuch-Quantenmechanik kann dies nicht leisten, und es gibt noch keine Einigkeit darüber, wie eine endgültige Quantenmechanik, die dies leistet, aussehen wird (siehe Goldstein 1998). Eine naheliegende Theorie ist die Bohmsche Mechanik, die nach ihrem Urheber David Bohm (1917-1992) benannt ist. Sie wird auch häufig als ,,pilot wave theory`` bezeichnet, weil in ihr eine ,,abstrakte Welle`` die Bewegung von Teilchen erzeugt. Bohmsche Mechanik ist auch ein Gesetz für die Bewegung von Teilchen, Bohmschen Teilchen, nicht Newtonschen, das bedeutet, waß das Gesetz für die Bewegung nicht Newtonsch ist.
Das Merkmal dieser Theorie ist, daß sie schon gar nicht mehr im physikalischen 3-dimensionalen Raum formuliert wird, sondern gleich im Phasenraum, wobei aber der Phasenraum der Bohmschen Mechanik in diesem Fall nicht 6N-dimensional, sondern nur noch 3N-dimensional ist, d.h. die Bewegung der Teilchen ist bereits eindeutig bestimmt, wenn man alle Orte kennt. Der 3N-dimensionale Raum, in dem die Teilchenorte abgetragen werden, heißt traditionell auch Konfigurationsraum (siehe Abbildung 9)
In der Bohmschen Mechanik ist also der Phasenraum
der Konfigurationsraum. Das Gesetz für die
Bewegung der Teilchen wird mit der
Schrödingerschen Wellenfunktion
![]() ( auch
( auch ![]() -Funktion
genannt) formuliert, die eine ,,abstrakte Welle``
auf dem Konfigurationsraum darstellt. Sie gehorcht
einer Wellengleichung (analog zum Newtonschen
Gravitationspotential, das der Potentialgleichung
genügt), der berühmten Schrödingergleichung.
-Funktion
genannt) formuliert, die eine ,,abstrakte Welle``
auf dem Konfigurationsraum darstellt. Sie gehorcht
einer Wellengleichung (analog zum Newtonschen
Gravitationspotential, das der Potentialgleichung
genügt), der berühmten Schrödingergleichung.

Abbildung 10: Eine ebene Welle fällt auf einen Doppelspalt.
Von den Spalten ausgehend entstehen Kugelwellen,
die sich überlagern (interferieren).
Die ![]() -Funktion hat Welleneigenschaften, sie
kann sich auslöschen (destruktive Interferenz)
oder verstärken (konstruktive Interferenz).
Betrachtet man nur ein einziges Teilchen, dann ist
die
-Funktion hat Welleneigenschaften, sie
kann sich auslöschen (destruktive Interferenz)
oder verstärken (konstruktive Interferenz).
Betrachtet man nur ein einziges Teilchen, dann ist
die ![]() -Funktion eine Welle im 3-dimensionalen
Raum, in welchem man das Wellenbild und die
Teilchenbahnen des Teilchens, d.h. den Fluß (die
Gesamtheit aller Bahnen des Teilchens auf dem
Konfigurationsraum, der für ein einzelnes Teilchen
gerade dem physikalischen Raum gleicht),
veranschaulichen kann.
-Funktion eine Welle im 3-dimensionalen
Raum, in welchem man das Wellenbild und die
Teilchenbahnen des Teilchens, d.h. den Fluß (die
Gesamtheit aller Bahnen des Teilchens auf dem
Konfigurationsraum, der für ein einzelnes Teilchen
gerade dem physikalischen Raum gleicht),
veranschaulichen kann.
Ich möchte das Bewegungsgesetz der Teilchen nicht
detailliert aufschreiben (siehe z. B. Bell
1987, Dürr, Goldstein, Zanghi 1992 und
1996). Für die Anschauung genügt es zu sagen,
daß sich die Bahnen in den Wellenbergen und
Tälern (im hoch-dimensionalen Konfigurationsraum)
häufen, und daß es dort, wo die ![]() -Funktion
verschwindet, keine Bahnen gibt.
-Funktion
verschwindet, keine Bahnen gibt.
Die Abbildung 11 zeigt die möglichen Bahnen eines
Bohmschen Teilchens bei dem sogenannten
Zwei-Spalt-Experiment: Ein Teilchen wird auf zwei
mikroskopisch kleine Spalte geschickt. Die das
Teilchen führende ![]() Funktion verhält sich
nach den zwei Spalten wie jede Welle: Es wird ein
Interferenzmuster nach dem Huygensschen Prinzip
erzeugt (Abbildung 10).
Funktion verhält sich
nach den zwei Spalten wie jede Welle: Es wird ein
Interferenzmuster nach dem Huygensschen Prinzip
erzeugt (Abbildung 10).
Die Stellen ohne Teilchenbahnen zeigen, wo die Interferenz die Welle ausgelöscht hat.

Abbildung 11: Die möglichen Bahnen eines Bohmschen
Teilchens beim Zwei-Spalt-Experiment. Die
Endpunkte der Bahnen sind das berühmte
Interferenzmuster des Zweispalt-Experimentes. In
jedem ,,Lauf`` des Experimentes, bei dem ein
Teilchen auf den Weg geschickt wird, erhält man
auf einer am rechten Ende aufgestellten Photoplatte
eine zufällige punktuelle Schwärzung (siehe
Abbildung 12), die der Endpunkt einer zufällig
ausgewählten Bahn der gezeigten möglichen Bahnen
ist.
Die für Wellen typische Ausbreitung nach allen Seiten sorgt dafür, daß die Bohmschen Bahnen in einem idealen Sinne instabil oder moderner gesagt, chaotisch sind: Was man sich am Galtonschen Brett mühsam klarmachen mußte, liefert die Bohmsche Mechanik fast umsonst. Dies zeigt Abbildung 11 ganz deutlich: Direkt hinter dem Spalt fächern die Teilchenbahnen auf so weit es geht, und trennen sich (vergleiche Abbildung 3).
Eine häufig gestellte Frage ist, ob man die Bahnen im Zweispaltexperiment ``sehen`` kann. Gemeint ist dabei, ob man die Bahn eines Teilchens durch einen der beiden Spalte hindurch sichtbar machen kann (z. B. in einer Nebelkammer), ohne daß sich am Auftreffmuster auf der Photoplatte (Abbildung 12) etwas ändert. In der Bohmschen Mechanik ist das unmöglich, weil jede Wechselwirkung mit dem Teilchen--und das Betrachten der Teilchenbahn ist eine Wechselwirkung--eine Beschreibung auf dem Konfigurationsraum des umfassenden Systems, welches aus Teilchen und ,,betrachtendem Gerät`` besteht, erforderlich macht. Die neue Wellenfunktion ist dann eine auf diesem Konfigurationsraum, was bedeuted, daß die Interferenzmöglichkeit zerstört wird.
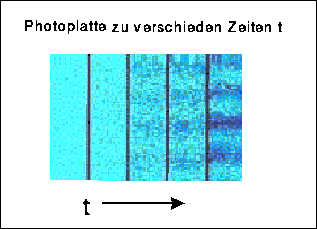
Abbildung 12: Im Laufe der Zeit bilden die zufälligen Auftreffpunkte
der Teilchen, die nacheinander den Doppelspalt
passieren, ein Interferenzmuster, wie es bei
Welleninterferenz auftritt. Die relativen
Häufigkeiten für die Auftreffpunkte werden durch
das Absolutquadrat der Wellenfunktion bestimmt.
Wie es der Zufall will, wurde Quantenmechanik
bereits seit der Erfindung der
Schrödinger-Gleichung als statistische Theorie
angesehen, allerdings ohne daß eine Verknüpfung
mit den Boltzmannschen und Gibbsschen Ideen
hergestellt wurde. Der Physiker Max Born
(1882-1970) postulierte, daß
![]() die
Wahrscheinlichkeitsverteilung der Orte der Teilchen
angibt. In der Tat beruhte dieses Postulat auf der
sogenannten Quantenflußgleichung, die von
Schrödinger (1887-1961) gefunden wurde und ganz
analog zum Liouvilleschen Theorem zu sehen ist.
Diese besagt, daß die Gewichtung eines jeden
Punktes des Konfigurationsraums mit
die
Wahrscheinlichkeitsverteilung der Orte der Teilchen
angibt. In der Tat beruhte dieses Postulat auf der
sogenannten Quantenflußgleichung, die von
Schrödinger (1887-1961) gefunden wurde und ganz
analog zum Liouvilleschen Theorem zu sehen ist.
Diese besagt, daß die Gewichtung eines jeden
Punktes des Konfigurationsraums mit
![]() ein Volumenmaß
ergibt, das von der Bohmschen Dynamik selbst
ausgezeichnet ist, nämlich ,,stationär`` ist (in
einem etwas allgemeineren als dem üblichen Sinne,
was für unsere Diskussion unerheblich ist).
Hiermit haben wir ein physikalisches Beispiel eines
von der Physik ausgezeichneten Inhaltes von Mengen,
welcher anders als in der klassischen Mechanik und
des Liouvilleschen Theorems nicht mehr durch den
gewöhnlichen Rauminhalt gegeben ist.
ein Volumenmaß
ergibt, das von der Bohmschen Dynamik selbst
ausgezeichnet ist, nämlich ,,stationär`` ist (in
einem etwas allgemeineren als dem üblichen Sinne,
was für unsere Diskussion unerheblich ist).
Hiermit haben wir ein physikalisches Beispiel eines
von der Physik ausgezeichneten Inhaltes von Mengen,
welcher anders als in der klassischen Mechanik und
des Liouvilleschen Theorems nicht mehr durch den
gewöhnlichen Rauminhalt gegeben ist.
Das Bornsche Postulat ist ganz analog zum Gibbsschen Ansatz. Man wird sich fragen, warum dieser Zusammenhang nicht gleich erkannt wurde. Ein Grund dafür liegt darin, daß in der Newtonschen statistischen Mechanik unserer Welt die Gibbssche Hypothese meistens falsch ist: Es herrscht kein thermisches Gleichgewicht. Die Bornsche Hypothese schien dagegen ausnahmslos richtig zu sein: Es herrscht immer ,,Quantengleichgewicht``. Das hätte zu der Überzeugung führen sollen, daß nun das Boltzmannsche Programm durchführbar ist.
Abbildung 13: Unser Universum ist im
Quantengleichgewicht.
Erst bei dem Physiker John S. Bell (1928-1990)
findet man das Selbstverständliche kurz und
selbstredend bemerkt (Bell 1987, vorher
spricht Bell von der Bahn eines atomaren Teilchens,
dem ![]() - Teilchen in einer Nebelkammer):
- Teilchen in einer Nebelkammer):
Suppose, for example, this world contains an actual ensemble of similar experimental set-ups. In the same way as for the-particle track it follows from the theory that the ,,typical`` world will approximately realize quantum mechanical distributions over such approximately independent components. The role of the hypothetical ensemble is precisely to permit definition of the word ,,typical``.
Die Ausarbeitung dieser wenigen Zeilen ist dann
allerdings ziemlich aufwendig, aber nicht mehr als
das (Dürr, Goldstein, Zanghi 1992 ).
Begrifflich war von Bell eigentlich schon alles
gesagt: Die Konfiguration der Bohmschen Teilchen
unseres Universums ist bezüglich des
![]() -Volumens typisch , wobei natürlich
-Volumens typisch , wobei natürlich
![]() die Wellenfunktion unseres Universums
darstellt. Es ist also so, daß in diesem Falle das
physikalische Bewegungsgesetz der Bohmschen
Teilchen die Anfangskonfiguration bestimmt,
nämlich als typische Konfiguration. Anders als in
Abbildung 8 kann nun ohne ,,äußere Hilfe`` die
Anfangsbedingung blind dem Bohmschen Gesetz folgend
ausgewählt werden, was in Abbildung 13
zum
Ausdruck gebracht werden soll.
die Wellenfunktion unseres Universums
darstellt. Es ist also so, daß in diesem Falle das
physikalische Bewegungsgesetz der Bohmschen
Teilchen die Anfangskonfiguration bestimmt,
nämlich als typische Konfiguration. Anders als in
Abbildung 8 kann nun ohne ,,äußere Hilfe`` die
Anfangsbedingung blind dem Bohmschen Gesetz folgend
ausgewählt werden, was in Abbildung 13
zum
Ausdruck gebracht werden soll.
Es ist hiermit keineswegs gesagt worden, daß unser Universum, quantenmechanisch gesehen, typisch ist! Nach wie vor ist unser Universum speziell, nur ist diese Spezialität verschoben worden, von den Teilchenkoordinaten hin zur Wellenfunktion. Es ist die Wellenfunktion des Universums, die für das thermische Nichtgleichgewicht unseres Universums verantwortlich ist. Die Teilchen des Bohmschen Universums aber sind ,,im Gleichgewicht`` mit der sie führenden Wellenfunktion.
Danksagung
Für die Korrektur und für viele
lehrreiche Gespräche über die Grundlagen dieses
Artikels möchte ich mich bei Reinhard Lang
bedanken.