Forschungsgruppe TQA
Forschungsthema Rucksackproblem
Problemstellung
Das Rucksackproblem (englisch: knapsack problem) ist unter den 21 klassischen NP-vollständigen Problemen womöglich das bekannteste. Es geht darum, aus einer Menge von Items, denen jeweils ein Gewicht und ein Wert zugeordnet ist, eine Teilmenge zu auswählen, die einerseits einer Gewichtsschranke genügt, also irgendwo 'hineinpasst', und andererseits mit ihrem Gesamtwert unter all den möglichen zu wählenden Teilmengen und deren Gesamtwerten ein Maximum darstellt.
Rucksackproblem in einer Dimension
Beim klassischen eindimensionalen Rucksackproblem hat jedes Item i einen Wert vi und ein Gewicht wi. Die gesuchte Teilmenge S ⊂ I = {1 … n} aller Items i passt in einen Rucksack, der ein Gesamtgewicht b aufnehmen kann (∑{i ∈ S} wi ≤ b) und hat unter diesen maximalen Wert ∑{i ∈ S} vi. Ein beliebter, einfacher Lösungsalgorithmus basiert auf Dynamischer Programmierung. In einer Matrix werden alle Optimalwerte für kleinere Rucksäcke gesammelt, also für alle Schranken 1 ≤ j ≤ b und für jede Anzahl von Items 1 ≤ i ≤ n. Man startet bei einem Item und erschließt sich größere Rucksäcke aus zuvor betrachteten kleineren Rucksäcken. Diese Methode vermindert die Laufzeit auf O(b·n), das Rucksackproblem ist also pseudopolynomiell. Schon bei vergleichsweise kleineren und realistisch vorkommenden Instanzen mit n = 60 Items und einer Schranke von b = 600 zeigt der Wechsel von einer Brute-Force-Baumsuche (alle möglichen Kombinationen von Items werden betrachtet und verglichen) auf Dynamische Programmierung einen deutlichen Benefit: Die Rechenzeit schrumpft von über 30 Jahren (grob geschätzt) auf eine Sekunde (programmiert in Java).
Neben anschaulichen Beispielen wie dem Packen eines Wanderrucksacks mit nützlichem Equipment gibt es offensichtlich in Wirtschaft und Industrie eine Vielzahl von Anwendungsmöglichkeiten. Speziell genannt sei hier auch die Spaltengenerierung bei der Lösung des Cutting Stock Problems von Gilmore und Gomory, bei der sich jeweils ein Rucksackproblem stellt.
Rucksackproblem in zwei Dimensionen
Die Forschungsgruppe TQA hat in enger Zusammenarbeit mit der Firma PerfectPattern GmbH einen Algorithmus für die Druckbranche entwickelt: Druckaufträge wie Poster, Plakate, Flyer und Visitenkarten werden kostenoptimal auf Sammelformen angeordnet. Da bei der Ermittlung der Kosten unter anderem auch die jeweiligen Auflagen und die Rüstkosten eine große Rolle spielen, handelt es sich dabei um eine Version des Cutting Stock Problem With Minimal Pattern, zusammen mit einer Unzahl an druckspezifischen Nebenbedingungen. Eine zweidimensionale Variante des Rucksackproblems erweist sich daher nicht nur aus akademischen Gründen als interessant, sondern auch zur Verifikation von kleinen Instanzen sowie als Teil des Lösungsalgorithmus zum Cutting Stock Problem With Minimal Pattern:Die Items sind kleine Rechtecke und haben statt einem Gewicht je eine Länge li und eine Höhe hi, sowie einen Wert vi der oft der Fläche entspricht. Sie dürfen je bi-oft verwendet werden. Man sucht nun eine Teilmenge S der Items I = {1 … n} und Vielfachheiten aj ≤ bj für alle j ∈ S, die mit den Vielfachheiten auf eine Platte der Länge L und der Höhe H passt und den Wert ∑{j ∈ S} aj vj maximiert. Oft wird zusätzlich gefordert, dass das Schnittmuster guillotinierbar ist: Wenn die platzierten Items aus der Platte herausgeschnitten werden, ist es nur möglich, Schnitte längs oder quer durch die ganze Platte oder durch zuvor entstandenen Teilplatten zu machen, was z.B. in der Papierverarbeitung sowie Holz- oder Glasindustrie nicht anders möglich ist.
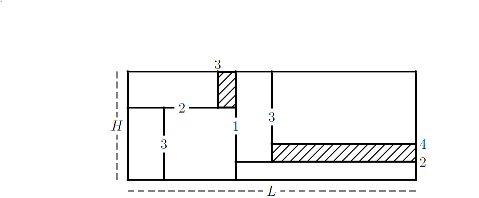
Abbildung 1: Zweidimensionales Schnittmuster mit nummerierten Guillotine-Cuts und schraffiertem Verschnitt

Abbildung 2: Nicht guillotinierbares Schnittmuster, das nicht durch eine Abfolge von Längs-/Querschnitten über die gesamte Breite entstehen kann.
Eine Arbeit von Christofides und Hadjiconstantinou ([1], Vorarbeit in [2]) beschreibt einen interessanten Algorithmus, der durch rundenweise Relaxierung des Zustandsraumes sehr gute obere Schranken findet. Die oberen Schranken sind guillotinierbare Schnittmuster, bei denen einzelne Rechtecke unzulässig oft - also öfter als bi-mal - vorkommen. In jeder Runde erhalten die Rechtecke andere Gewichte: Zunächst sind diese 0 und sie erhöhen sich, falls ein Rechteck in einer vorigen oberen Schranke zu oft verwendet wurde. Der Algorithmus bricht ab, wenn eine obere Schranke zulässig und somit optimale Lösung ist, oder mündet nach einer zuvor bestimmten Anzahl von Relaxierungsdurchläufen in eine Branch-And-Bound-Suche, bei der die beste zuvor gefundene obere Schranke wiederverwendet wird.
Die beste obere Schranke verkürzt natürlich die Branch-and-Bound-Suche, hin und wieder findet man bei einer günstigen Gelegenheit bereits in den Relaxierungsrunden eine zulässige obere Schranke. Dies verkürzt die Rechenzeit durch den Wegfall der Baumsuche enorm (ein solches Beispiel ist in [1] angegeben). Aktuelle Forschung in der Forschungsgruppe TQA beschäftigt sich daher unter anderem mit der Erweiterung dieses Algorithmus und der Vermehrung besagter günstiger Gelegenheiten.
Literatur:
[1] N. Christofides, E. Hadjiconstantinou: An exact algorithm for orthogonal 2-D cutting problems using guillotine cuts. European Journal of Operational Research (1995) 83 (1), 21-38
[2] N. Christofides, C. Whitlock: An algorithm for two-dimensional cutting problems. Operations Research 25.1 (1977): 30-44.

