Forschungsgruppe TQA
Forschungsthema Cutting Stock Problem
Problemstellung
Das Cutting Stock Problem hält, was der Name verspricht: Es geht darum, Stöcke so zu zerschneiden, dass möglichst wenig Verschnitt entsteht. (Der englische Ausdruck 'stock' umfasst natĂĽrlich mehr: Allgemeine Teile mit einer geometrischen Ausdehnung sollen geeignet zerschnitten werden. Im Deutschen beschreibt der Begriff 'Zuschnittproblem' den Sachverhalt des 'Cuttung Stock Problem' adäquat.)
Cutting Stock Problem in einer Dimension
Bei dem Zuschneiden der Stöcke sollen kleinere Stöcke entstehen, deren Länge und jeweilige Anzahl vorgegeben ist, die also aus den großen Stöcken produziert werden sollen. Die Optimierungsaufgabe ist, die Anzahl der großen Ausgangsstöcke zu minimieren, mit dem Ziel möglichst wenig Rohmaterial zu verbrauchen. Als Beispiel kann man sich ganz praktisch eine Baustelle vorstellen, bei der Rohre verschiedener Länge gebraucht werden, die aus 10 Meter langen Ausgangsrohren entstehen. Natürlich möchte man den Verschnitt minimieren, und dadurch die Kosten für die benötigten Ausgangsrohre reduzieren.
Mathematisch formuliert heiĂźt dies, das man n unterschiedliche Items bzw. kleine Stöcke betrachtet, die jeweils die Länge li, 1 ≤ i ≤ n, haben und die bi-oft gebraucht werden. Die Ausgangslänge des Rohmaterials (also der großen Stöcke) sei L und es gelte li ≤ L für alle i mit 1 ≤ i ≤ n. Ein Zuschnitt z ist eine Vorschrift, wie die kleinen StĂĽcke aus dem Ausgangsmaterial geschnitten werden, also zum Beispiel 'dreimal das erste StĂĽck und zweimal das dritte'. Dieser Sachverhalt lässt sich durch einen Vektor z beschreiben: (3,0,2, ...) = (z1, ... ,zn) = z. Dabei muss natĂĽrlich gelten, dass dies von der Länge her machbar ist, dass also in dem Beispiel gilt: 3·l1 + 2·l3 + ... ≤ L. Die Menge Z dieser Zuschnitte ist typischerweise sehr groß, selbst wenn man sich bemĂĽht, unlogische Zuschnitte zu entfernen - beispielsweise solche, die viermal ein Teil der Länge li produzieren, welches man nur bi = 3-mal benötigt. Eine allgemeine Formel oder eine übersichtliche Abschätzung zur Anzahl der möglichen Zuschnitte anzugeben ist wegen der Extremfälle nicht einfach. Wir nennen diese Anzahl zur Veranschaulichung für ein festes Beispiel: Gegeben seien 20 Items der Längen 1,2,3, ... 20 die jeweils füffach aus Stöcken der Länge 200 geschnitten werden sollen. Dann gibt es 325.984.522.513 mögliche Zuschnitte.
Ein zulässiges Produktionslayout C zu einer Instanz (d.h. zu der Vorgabe von n unterschiedlichen Items, die jeweils die Länge li, 1 ≤ i ≤ n, haben und die bi-oft aus Items der Länge L produziert werden sollen) beinhaltet endlich viele verschiedene Zuschnitte z ∈ Z mit der Information, dass der Zuschnitt z jeweils xz oft auf das Rohmaterial angewandt werden soll (xz ist dabei eine natĂĽrliche Zahl für z ∈ C). Die dadurch entstandenen kleinen StĂĽcke genĂĽgen dem Bedarf:
bi ≤ ∑{z ∈ C} xz·zi ∀ i.
Ein optimales Produktionslayout - also eine Lösung des Optimierungsproblems, bei der der Ressourcenverbrauch minimal ist - muss noch der Forderung genĂĽgen, dass die Zielfunktion
C → ∑{z ∈ C} xz
einen minimalen Wert annimmt, denn das ist die Anzahl der Items der Länge L, die bei der Produktion mit dem Produktionslayout C verbraucht werden.
Das Cutting Stock Problem ist NP-schwer, weshalb man sich fĂĽr wirtschaftliche Anwendungen nicht mehr mit exakten Lösungsalgorithmen aufhält. Einen bahnbrechender Durchbruch auf der Suche nach guten und schnellen Heuristiken gab es in den 60er Jahren, als Gilmore und Gomory einen Algorithmus fĂĽr die stetige Relaxation (Zuschnitte z ∈ C dĂĽrfen hier xz-oft mit einer reellen Zahl xz verwendet werden) veröffentlichten. Sie entwickelten dabei die Simplexmethode der Linearen Programmierung weiter und kombinierten es mit einer effizienten Spaltengenerierung. Damit lieĂźen sich auch gute Näherungen fĂĽr das nicht relaxierte Problem finden. [P. C. Gilmore and R. E. Gomory: A Linear Programming Approach to the Cutting-Stock Problem, Operations Research, Vol. 9, No. 6 (Nov. - Dec., 1961), pp. 849-859]
Wie so oft in der Kombinatorischen Optimierung ist das Cutting Stock Problem sehr variantenreich. Nur kleine Abwandlungen an der Aufgabenstellung, oft inspiriert durch konkrete Probleme in Industrie und Wirtschaft, stellen die bereits gefundene Lösungsalgorithmen in Frage und verlangen nach neuen Ideen. Ein Beispiel ist die Forderung, dass die Produktionslayouts C keine Auftragsteilung zulassen soll, d.h. wenn z = (z1, ... ,zn) ∈ C ein Zuschnitt ist mit xz ≠ 0 und mit zk ≠ 0, für ein festes k (d.h. einige Stücke vom Item k werden mit diesem Zuschnitt produziert), dann ist die Produktion zum Item k mit diesem festen Zuschnitt z bereits erledigt:
bk ≤ xz·zk und es ist sk = 0 ∀ s ∈ C\{z} und dieses feste k.
Eine andere Variante ergibt sich in zwei Dimensionen:
Cutting Stock Problem in zwei Dimensionen
Das zweidimensionale Cutting Stock Problem tritt z.B. in der Papierbranche auf, wenn aus Papierbögen einzelne Poster, Plakate und Visitenkarten mit minimalen Verschnitt entstehen sollen. Es geht dann darum, auf ein großes Rechteck kleinere Rechtecke mit Vielfachheiten geeigent zu platzieren. Ebenso benötigt die Holzbranche Lösungen zu diesem Problem, und in beiden Bereichen wird oft die Zusatzbedingung nach speziellen Schnitten, sog. Guillotine Cuts gestellt. Zudem sei die Bekleidungsindustrie genannt, die aus langen Stoffbahnen Teile von Hemden, Hosen und Pullover schneidet, wobei die Formen keine Rechtecke, ja insbesondere nicht einmal mehr konvex sind. Man spricht in diesem Fall von Verschachtelung oder Nesting.
Cutting Stock Problem with Minimal Pattern
Das Cutting Stock Problem with Minimal Pattern (CSMP) hat seinen Ursprung ebenfalls in der konkreten Anwendung. Gehen wir zurück zu unserem Beispiel, bei denen aus langen Rohren kleinere Rohrstücke geschnitten werden. Man benötigt aus Ausgangsrohren von zehn Meter Länge zwei Stücke, die vier Meter lang sind und zwei Stücke, die fünf Meter lang sind. Bisher wäre es gleichwertig, ob man zwei gleiche Zuschnitte verwendet, wo je ein Stück mit Länge vier und eines mit Länge fünf herausspringt - oder ob man zwei unterschiedliche Zuschnitte verwendet, einen mit zweimal vier Meter und einen mit zweimal fünf Meter. In jedem Fall werden zwei Ausgangsrohre verbraucht. Sollte allerdings eine Zuschneidemaschine verwendet werden, muss diese bei zwei unterschiedlichen Zuschnitten einmal extra eingestellt werden, und es gilt, neben
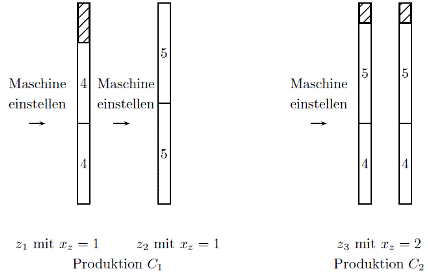
den Rohstoffkosten auch die RĂĽstkosten zu minimieren, also insbesondere den Zeitaufwand und die Personalkosten fĂĽr die Maschineneinstellung zu berĂĽcksichtigen.
Das Cutting Stock Problem with Minimal Pattern galt bis vor Kurzem als ungelöst. Die Forschungsgruppe TQA konnte allerdings in den letzten Jahren einen Lösungsalgorithmus entwickeln. Dieser Algorithmus stieĂź in der Druckindustrie auf groĂźes Interesse, da sich damit die Kosten der Produktion (beim Akzidendruck) in einem erheblichen Umfang durch die Einsparung von Ressourcen (Papier und Platten) reduzieren lassen. In Zusammenarbeit mit der Firma PerfectPattern GmbH wurde dieser Lösungsalgorithmus in einer Software fĂĽr die Druckbranche verwendet, dank der sich Druckformen effizient optimieren lassen: Es sollen Aufträge wie Poster, Plakate und Visitenkarten auf großen Offset-Druckmaschinen gemeinsam gedruckt werden. Dazu werden die Rechtecke zu den Aufträgen auf großen, rechteckigen Druckformen angeordnet, und die Druckplatten für die Druckmaschinen werden nach dieser Anordnung (oder Layout) belichtet. Mit diesen Platten werden dann so viele Druckbögen gedruckt, wie es die Auflagen der Aufträge auf der Druckform erfordert. Solch eine Druckform mit mehr als einem Auftrag nennt man Sammelform - man kann sie sich eine solche Sammelform bzw. die nach der Sammelform belichtete Druckplatte als relativ kostenintensive "Schablone" vorstellen, die jeweils die Farbe aufnimmt und auf jedem zu bedruckenden Bogen aufträgt.
Hier zeigt sich der Unterschied zum normalen Cutting Stock Problem, da die RĂĽstkosten insbesondere in der Produktion teurer Sammelformen (Druckplatten) niedrig gehalten werden sollen wie auch der Personalaufwand beim Rüsten und die Stillstandszeiten. Die unterschiedlichen Auflagen verbieten es, die Aufträge auf Sammelformen so zu platzieren dass die lediglich freie Fläche minimiert wird: Hat man am Ende ein Poster mit hoher Auflage und eine Visitenkarte mit vergleichsweise niedriger Auflage auf derselben Sammelform, wird man trotzdem so oft drucken müssen, bis genügend Poster vorhanden sind. Die überschüssigen Visitenkarten muss man wegwerfen.
Die so entstandene Software (sPrint One) wird bereits erfolgreich in Firmen eingesetzt - die standardisierte API findet sich unter http://www.perfectpattern.de/druck/sprint-one/apidocu. Der Einsatz dieser Software ist ein glänzendes Beispiel dafür, wie sich Kosten 'nur' durch Verwendung mathematischer Ideen senken lassen.
Standard: http://www.perfectpattern.de/druck/sprint-one/apidocu

