
Kapitel IV, §21
1o C(I), der R-Vektorraum der stetigen Funktionen auf einem Intervall I mit Werten in R mit der üblichen
Multiplikation (punktweise)
2o Im Falle der Existenz ist die Inverse zu h eindeutig bestimmt und wird auch mit h-1 bezeichnet.
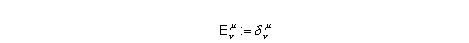
In dem für uns wichtigen
Falle der Algebra Knxn der (n,n)-Matrizen ist die Einheitsmatrix E (= E(n) ) mit .
Bemerkung: .
1o Eine Eins ist im
Falle der Existenz eindeutig bestimmt und wird auch mit 1 bezeichnet (nicht verwechseln mit 1 in K
!).
Die invertierbaren Matrizen
in Knxn sind die Matrizen, die einen Isomorphismus definieren, und das sind die Matrizen mit
Rang n.
ist eine assoziative und
kommutative R-Algebra mit Eins: 1(x) = 1.
Die invertierbaren Elemente
sind genau die Funktionen f ohne Nullstelle und die Inverse
ist dann

