Seminar Algorithmische Algebraische ZahlentheorieSommersemester 2019 |
Warum dieses Seminar?
In Vorlesungen, Übungen und Klausuren wird suggeriert, dass die einzige Aufgabe der Mathematiker sei, mathematische Aussagen zu beweisen. In Wirklichkeit, und dieser Teil wird im Studium meist ausgespart, beginnt die Bearbeitung einer mathematischen Fragestellung zuerst damit, die Aussagen zu finden, die man beweisen möchte. Aber wie kommen wir zu diesen? Eine Methode ist das Rechnen von verschiedenen Beispielen bzw. die Betrachtung von Spezialsituationen, an denen wir hoffen gewisse Muster erkennen können. Zum Beispiel ist von Gauß überliefert, dass er eine große Menge an Rechnungen durchgeführt hat, bevor er Beweise angegangen ist, was zur damaligen Zeiten viel Geduld und enormes Geschick erforderte.
Heute ist unsere Situation um einiges besser, denn wir können uns durch Computer bei der Berechnung von Beispielen unterstützen lassen und gerade die Algebra und Zahlentheorie eignet sich hervorragend für Rechnungen mit Computern, da sich die dort behandelten Objekte oft einfach am Computer repräsentieren lassen.
Natürlich kann man sich jetzt auf den Standpunkt stellen, jemand würde schon ein geeignetes Programm schreiben, das man dann als black box benutzen kann. Mathematiker sollten aber danach streben, sich auch dafür zu interessieren, was in einer solchen black box passiert. Außerdem bietet ein genaueres Verständnis die Möglichkeit vorhandene Routinen besser an ein gegebenes Problem anpassen zu können.
Und genau aus diesen Gründen streben wir in diesem Seminar ein besseres theoretisches Verständnis von bekannten Algorithmen auf dem Teilgebiet der Algebraischen Zahlentheorie an.
Was ist Algebraische Zahlentheorie?
Elementare Zahlentheorie kann man als die Beschäftigung mit den Eigenschaften der ganzen Zahlen \(\mathbb{Z}\) ansehen. Allgemeiner beschäftigt sich nun Algebraische Zahlentheorie mit einem zu \(\mathbb{Z}\) analogem Objekt, dem Ganzheitsring \(\mathcal{O}_{K}\), welcher in einer endlichen Erweiterung \(K\) von \(\mathbb{Q}\) definiert ist.1
Im Ring \(\mathcal{O}_{K}\) kann man jetzt natürlich das Verhalten von Primidealen studieren und überlegen, ob für diese ähnliche Eigenschaften wie für Primzahlen in \(\mathbb{Z}\) gelten. Außerdem kann man eine Invariante von \(\mathcal{O}_{K}\), die sogenannte Klassenzahl definieren, die unter anderem Auskunft über die algebraischen Eigenschaften des Rings gibt. Zum Beispiel ist der Ring \(\mathcal{O}_{K}\) genau dann ein Hauptidealring, wenn die Klassenzahl \(1\) ist.
In diesen allgemeineren Ringen treten aber noch andere Fragestellungen auf, die für die ganzen Zahlen \(\mathbb{Z}\) uninteressant sind: Zum Beispiel kann man sich in \(\mathcal{O}_{K}\) für die Struktur der Einheitengruppe interessieren oder ob ein gegebenes Ideal ein Hauptideal ist.
Und warum jetzt Algorithmische Algebraische Zahlentheorie?
Schon seit dem 19. Jahrhundert kennt man folgende Ergebnisse:
- \(\mathcal{O}_{K}\) hat (als \(\mathbb{Z}\)-Modul) den \(\mathbb{Z}\)-Rang \([K:\mathbb{Q}]\).
- Im Ring \(\mathcal{O}_{K}\) hat jedes Ideal \(I\) eine eindeutige endliche Primidealzerlegung, z.B. \[I= \mathfrak{p}^{n_{1}}_{1} \cdots \mathfrak{p}^{n_{s}}_{s}\]
- Für die Einheiten \(\mathcal{O}_{K}^{\times}\) des Rings \(\mathcal{O}_{K}\) gilt: \[\mathcal{O}_{K}^{\times} \cong \mu(K) \times \mathbb{Z}^{r}\] wobei \(\mu(K)\) eine endliche zyklische Gruppe in \(K\) ist und \( r < [K:\mathbb{Q}] \) .
- Die Klassenzahl eines Ganzheitsrings \(\mathcal{O}_{K}\) ist endlich.
Die Frage ist nun: Wie müssen wir vorgehen, wenn wir konkret den Ganzheitsring, die Primideale, die Einheiten oder die Klassenzahl für ein gegebenes \(K\) berechnen wollen? Genau solche Fragen wollen wir in diesem Seminar beantworten.
Tatsächlich ist es so, dass es keine bekannte Algorithmen gibt, die die letzten beiden Probleme in polynomialer Laufzeit lösen. Aber gerade dieser Umstand macht es besonders wichtig sich gute Algorithmen zu überlegen um die genannten Objekte zu berechnen.
Ein Grund warum wir uns genau für diese Objekte in der Algebraischen Zahlentheorie interessieren, ist, dass man viele andere Fragestellungen mit den hier behandelten Techniken und Methoden bearbeiten kann. Tatsächlich werden die hier beschrieben Probleme deswegen auch als die Hauptprobleme der Algorithmischen Algebraischen Zahlentheorie bezeichnet.
Gibt es auch Zusammenhänge zu Themen außerhalb der Reinen Mathematik?
Ja! Fast alle oben beschriebenen Fragestellungen haben auch kryptographische Anwendungen. Außerdem gibt es in den letzten Jahren auch Ideen wie man die genannten Probleme auf Quantencomputern in polynomialer Laufzeit2 lösen könnte.
Formales/Voraussetzungen
Grundsätzlich handelt es sich um ein Seminar, dass Sie sowohl im Bachelor als auch im Master Mathematik einbringen können. Bitte geben Sie aber vor der Themenwahl bekannt, ob Sie das Seminar in den Bachelor oder Master Mathematik einbringen wollen, damit wir das bei der Themenvergabe berücksichtigen können.
Um zu entscheiden, ob Sie für das Seminar geeignet sind, gibt es folgende Hilfe:
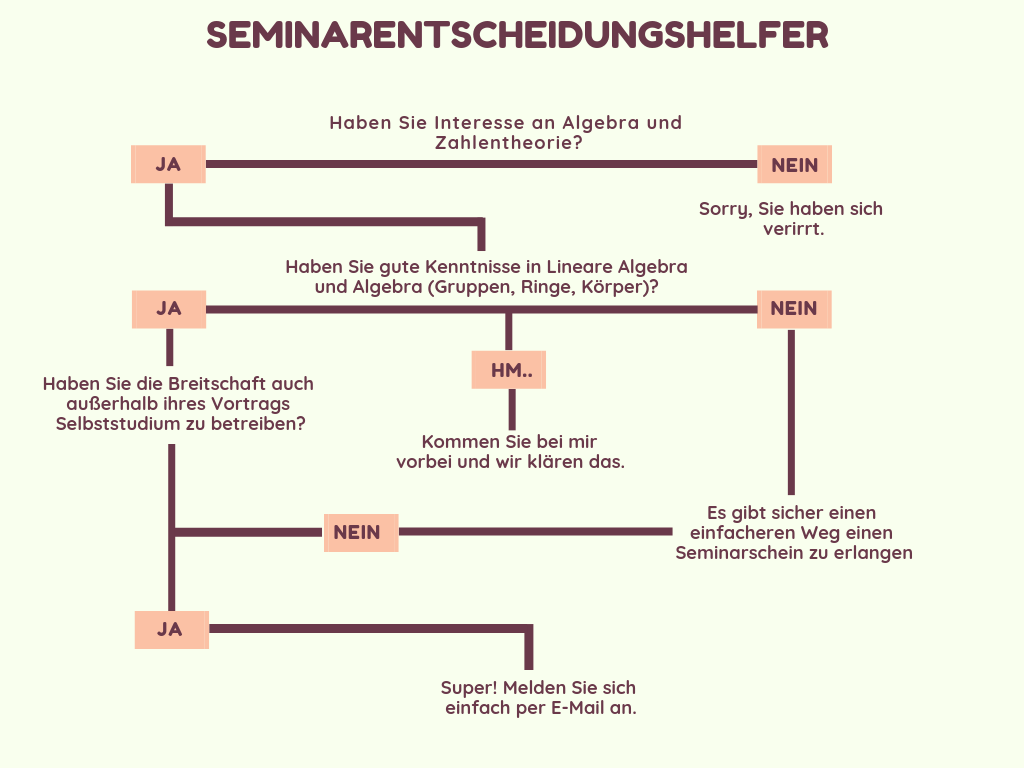
Insbesondere ist das Seminar so konzipiert, dass es möglich ist, es parallel zur Höheren Algebra zu besuchen. Es bietet auch eine gute Grundlage falls man im Wintersemester 2019/20 die Algebraische Zahlentheorie besuchen will.
Aber auch Studenten mit mehr Vorkenntnissen (z.B. Algebraische Zahlentheorie) können von diesem Seminar profitieren, da algorithmische Aspekte in den Wahlpflichtmodulen meist keine große Rolle spielen.
Vortragsthemen
Das Ziel dieses Seminar ist es Algorithmen der Algebraischen Zahlentheorie kennen zu lernen und zu verstehen.
Das Seminar folgt hier vorwiegend (Pohst 1993).
In (Cohen 1993) finden Sie auch alle besprochenen Themen in einer etwas ausführlicheren Darstellung.
Wir setzen dabei aber nicht voraus, dass wir die zu berechnenden Objekte schon kennen.
Aus praktischen und zeitlichen Gründen wollen wir uns aber mit der Berechnung von Objekten der Linearen Algebra und Algebra die wir für die Algorithmen in der Algebraischen Zahlentheorie brauchen nur
überblicksartig auseinander setzen.
Die folgende Liste von Vortragsthemen enthält jeweils eine Aufzählung der Mindestbestandteile des Vortrags.
Darüber hinaus können, falls es die Zeit zulässt, auch noch andere Dinge der betreffenden Kapitel eingebaut werden.
Genaueres besprechen in der Vorbesprechung Ihres Vortrags
Dieser Vortrag besteht aus zwei Teilen. Im ersten Teil wollen wir unsere Kenntnisse der Linearen Algebra festigen.
Im zweiten Teil wollen wir einen Einblick in die so genannte Geometrie der Zahlen gewinnen und zwei ihrer Hauptsätze kennen lernen.
Hermite-Normalform
- Definition und Existenz Hermite-Normalform evtl. mit Beweis von Theorem III.1.3 in (Pohst 1993) aber benutze Lemma ohne Beweis3
- Definition und Existenz Smith-Normalform d.h. Theorem III.1.5 in (Pohst 1993) (ohne Beweis)
Grundlagen zu Gittern
- Definition Gitter, Determinante eines Gitters und fundamentales Parallelotop (p. 14 (Pohst 1993))
- Minkowskischer Gitterpunktsatz (ohne Beweis4)
- Definition aufeinander folgende Minima und zweiter Satz von Minkowski (Theorem III.2.4 in (Pohst 1993), ohne Beweis)
In diesen beiden Vorträgen werden wir einen bekannten Algorithmus von Lenstra, Lenstra und Lovasz und einige Anwendungen davon studieren.
Dieser hat auch außerhalb der Algorithmischen Algebraischen Zahlentheorie einige Anwendungen.
Die genaue Aufteilung der beiden Vorträge besprechen wir dann in einer Vorbesprechung.
Reduktion
- Definition Minkowski reduzierte und LLL-reduzierte Basis (p. 16) in (Pohst 1993)
- LLL-Algorithmus (Algorithmus III.3.5 in (Pohst 1993))
- MLLL-Algorithmus (Algorithmus III.3.8 in (Pohst 1993))
Aufzählung von Gitterpunkten
- Algorithmus für Quadratische Ergänzung (Algorithmus III.4.1 in (Pohst 1993))
- Algorithmus zur Bestimmung von Gitterpunkten (Algorithmus III.4.2 in (Pohst 1993))
Dieser Vortrag soll eine Einführung in die ersten Konzepte der Algebraischen Zahlentheorie geben.
Auf Beispiele soll hier großen Wert gelegt werden.
Es bietet sich zum Beispiel an, sich die eingeführten Objekte für quadratische Zahlkörper anzusehen,
i.e. für Körper der Form \(\mathbb{Q}(\sqrt{d})\).
- Definition: Zahlkörper, algebraische Zahlen, Ganzheitsring, Ordnung5, Ganzheitsbasis mit Beispielen (jedes Lehrbuch der Algebraischen Zahlentheorie z.B. (Neukirch 1992), (Cohen 2007), aber auch (Pohst 1993) und (Cohen 1993)).
- Definition Diskriminante von Polynom, Ganzheitsring, Zahlkörper mit einigen Eigenschaften und Beispielen (jedes Lehrbuch der Algebraischen Zahlentheorie z.B. (Neukirch 1992), (Cohen 2007), aber auch (Pohst 1993) und (Cohen 1993)).
- Arithmetische Operationen in Zahlkörper p.31-33 in (Pohst 1993).
Der Ganzheitsring ist eines der wichtigsten Objekte der Algebraischen Zahlentheorie.
Auch für uns ist er von entscheidender Bedeutung, weil er Basisobjekt der später zu berechnenden Invarianten ist.
Am Anfang der Überlegungen steht die Feststellung, dass ein Ganzheitsring die Maximalordnung eines Zahlkörpers \(K\) ist.
Die Strategie ist nun aus generischen Teilordnungen diese Maximalordnung zu erzeugen.
- Ganzer Abschluss (Kapitel V.1 in (Pohst 1993)), insbesondere das ein Lemma von Dedekind (Lemma V.1.4 in (Pohst 1993)).
- Überblick über die "Round 2"-Methode (Kapitel V.2 in (Pohst 1993))
- Überblick über die "Round 4"-Methode (Kapitel V.3 in (Pohst 1993))
In diesen beiden wollen wir die Einheitengruppe \(\mathcal{O}_{K}^{\times}\) eines Zahlkörpers \(K\) berechnen.
Ein natürlicher Startpunkt für die Untersuchungen ist ein wichtiger Struktursatz von Dedekind.
Dieser besagt, dass es einen Isomorphismus von Gruppen gibt: \[\mathcal{O}_{K}^{\times} \cong \mu(K) \times \left\langle E_{1} \right\rangle \times \cdots \times \left\langle E_{r} \right\rangle \cong \mu(K) \times \mathbb{Z}^{r},\]
wobei \(\mu(K)\) eine endliche zyklische Untergruppe von \(\mathcal{O}_{K}^{\times}\) ist.
Die Erzeuger von \(\left\langle E_{r} \right\rangle\) nennt man Fundamentaleinheiten.
Mithilfe dieser Fundamentaleinheiten können wir dann den Begriff des Regulators definieren und für ihn eine Schranke angeben.
Der nächste Arbeitschritt ist die Erzeugung von \(r\) unabhängigen Einheiten, wobei wir hier zwei Methoden kennen lernen werden.
Abgeschlossen wird dieser Abschnitt mit der Berechnung der Fundamentaleinheiten aus den \(r\) unabhängigen (schon gefundenen) Einheiten.
- Dirichletscher Einheitensatz und Definition Fundamentaleinheiten (ohne Beweis6, jedes Lehrbuch der Algebraischen Zahlentheorie e.g. (Neukirch 1992), (Cohen 2007) oder auch (Pohst 1993) und (Cohen 1993)).
- Definition Regulator und Schranke für den Regulator
- Berechnung von \(r\) unabhängigen Einheiten mit zwei unterschiedliche Methoden: Dirichlet und Lagrange Kapitel VI.2 in (Pohst 1993).
- Berechnung der Fundamentaleinheiten Kapitel VI.2 in (Pohst 1993).
Hier wollen wir zuerst die notwendigen Begriffe der Algebraischen Zahlentheorie einführen um die Klassengruppe eines Zahlkörpers definieren zu können.
Den Beweis, dass es sich hierbei um eine endliche abelsche Gruppe handelt soll skizziert werden.
Danach soll ein Überblick gegeben werden, wie man die Klassengruppe nun algorithmisch berechnen kann.
- Definition aller notwendigen Konzepte damit die Klassengruppe eines Zahlkörpers definiert werden kann. (jedes Lehrbuch der Algebraischen Zahlentheorie e.g. (Neukirch 1992), (Cohen 2007) oder auch (Pohst 1993) und (Cohen 1993))
- Rest von Kapitel VII.1 in (Pohst 1993) insbesondere Minkowskischranke.
- Überblick über eine Methode zur Berechnung der Klassengruppe (Kapitel VII.2 in (Pohst 1993)).
Das Ziel dieses Seminar ist es Algorithmen der Algebraischen Zahlentheorie kennen zu lernen und zu verstehen. Das Seminar folgt hier vorwiegend (Pohst 1993). In (Cohen 1993) finden Sie auch alle besprochenen Themen in einer etwas ausführlicheren Darstellung.
Wir setzen dabei aber nicht voraus, dass wir die zu berechnenden Objekte schon kennen.
Aus praktischen und zeitlichen Gründen wollen wir uns aber mit der Berechnung von Objekten der Linearen Algebra und Algebra die wir für die Algorithmen in der Algebraischen Zahlentheorie brauchen nur überblicksartig auseinander setzen.
Die folgende Liste von Vortragsthemen enthält jeweils eine Aufzählung der Mindestbestandteile des Vortrags. Darüber hinaus können, falls es die Zeit zulässt, auch noch andere Dinge der betreffenden Kapitel eingebaut werden. Genaueres besprechen in der Vorbesprechung Ihres Vortrags
Dieser Vortrag besteht aus zwei Teilen. Im ersten Teil wollen wir unsere Kenntnisse der Linearen Algebra festigen. Im zweiten Teil wollen wir einen Einblick in die so genannte Geometrie der Zahlen gewinnen und zwei ihrer Hauptsätze kennen lernen.
Hermite-Normalform
- Definition und Existenz Hermite-Normalform evtl. mit Beweis von Theorem III.1.3 in (Pohst 1993) aber benutze Lemma ohne Beweis3
- Definition und Existenz Smith-Normalform d.h. Theorem III.1.5 in (Pohst 1993) (ohne Beweis)
Grundlagen zu Gittern
- Definition Gitter, Determinante eines Gitters und fundamentales Parallelotop (p. 14 (Pohst 1993))
- Minkowskischer Gitterpunktsatz (ohne Beweis4)
- Definition aufeinander folgende Minima und zweiter Satz von Minkowski (Theorem III.2.4 in (Pohst 1993), ohne Beweis)
In diesen beiden Vorträgen werden wir einen bekannten Algorithmus von Lenstra, Lenstra und Lovasz und einige Anwendungen davon studieren. Dieser hat auch außerhalb der Algorithmischen Algebraischen Zahlentheorie einige Anwendungen. Die genaue Aufteilung der beiden Vorträge besprechen wir dann in einer Vorbesprechung.
Reduktion
- Definition Minkowski reduzierte und LLL-reduzierte Basis (p. 16) in (Pohst 1993)
- LLL-Algorithmus (Algorithmus III.3.5 in (Pohst 1993))
- MLLL-Algorithmus (Algorithmus III.3.8 in (Pohst 1993))
Aufzählung von Gitterpunkten
- Algorithmus für Quadratische Ergänzung (Algorithmus III.4.1 in (Pohst 1993))
- Algorithmus zur Bestimmung von Gitterpunkten (Algorithmus III.4.2 in (Pohst 1993))
Dieser Vortrag soll eine Einführung in die ersten Konzepte der Algebraischen Zahlentheorie geben. Auf Beispiele soll hier großen Wert gelegt werden. Es bietet sich zum Beispiel an, sich die eingeführten Objekte für quadratische Zahlkörper anzusehen, i.e. für Körper der Form \(\mathbb{Q}(\sqrt{d})\).
- Definition: Zahlkörper, algebraische Zahlen, Ganzheitsring, Ordnung5, Ganzheitsbasis mit Beispielen (jedes Lehrbuch der Algebraischen Zahlentheorie z.B. (Neukirch 1992), (Cohen 2007), aber auch (Pohst 1993) und (Cohen 1993)).
- Definition Diskriminante von Polynom, Ganzheitsring, Zahlkörper mit einigen Eigenschaften und Beispielen (jedes Lehrbuch der Algebraischen Zahlentheorie z.B. (Neukirch 1992), (Cohen 2007), aber auch (Pohst 1993) und (Cohen 1993)).
- Arithmetische Operationen in Zahlkörper p.31-33 in (Pohst 1993).
Der Ganzheitsring ist eines der wichtigsten Objekte der Algebraischen Zahlentheorie. Auch für uns ist er von entscheidender Bedeutung, weil er Basisobjekt der später zu berechnenden Invarianten ist. Am Anfang der Überlegungen steht die Feststellung, dass ein Ganzheitsring die Maximalordnung eines Zahlkörpers \(K\) ist. Die Strategie ist nun aus generischen Teilordnungen diese Maximalordnung zu erzeugen.
- Ganzer Abschluss (Kapitel V.1 in (Pohst 1993)), insbesondere das ein Lemma von Dedekind (Lemma V.1.4 in (Pohst 1993)).
- Überblick über die "Round 2"-Methode (Kapitel V.2 in (Pohst 1993))
- Überblick über die "Round 4"-Methode (Kapitel V.3 in (Pohst 1993))
In diesen beiden wollen wir die Einheitengruppe \(\mathcal{O}_{K}^{\times}\) eines Zahlkörpers \(K\) berechnen. Ein natürlicher Startpunkt für die Untersuchungen ist ein wichtiger Struktursatz von Dedekind. Dieser besagt, dass es einen Isomorphismus von Gruppen gibt: \[\mathcal{O}_{K}^{\times} \cong \mu(K) \times \left\langle E_{1} \right\rangle \times \cdots \times \left\langle E_{r} \right\rangle \cong \mu(K) \times \mathbb{Z}^{r},\] wobei \(\mu(K)\) eine endliche zyklische Untergruppe von \(\mathcal{O}_{K}^{\times}\) ist. Die Erzeuger von \(\left\langle E_{r} \right\rangle\) nennt man Fundamentaleinheiten. Mithilfe dieser Fundamentaleinheiten können wir dann den Begriff des Regulators definieren und für ihn eine Schranke angeben. Der nächste Arbeitschritt ist die Erzeugung von \(r\) unabhängigen Einheiten, wobei wir hier zwei Methoden kennen lernen werden. Abgeschlossen wird dieser Abschnitt mit der Berechnung der Fundamentaleinheiten aus den \(r\) unabhängigen (schon gefundenen) Einheiten.
- Dirichletscher Einheitensatz und Definition Fundamentaleinheiten (ohne Beweis6, jedes Lehrbuch der Algebraischen Zahlentheorie e.g. (Neukirch 1992), (Cohen 2007) oder auch (Pohst 1993) und (Cohen 1993)).
- Definition Regulator und Schranke für den Regulator
- Berechnung von \(r\) unabhängigen Einheiten mit zwei unterschiedliche Methoden: Dirichlet und Lagrange Kapitel VI.2 in (Pohst 1993).
- Berechnung der Fundamentaleinheiten Kapitel VI.2 in (Pohst 1993).
Hier wollen wir zuerst die notwendigen Begriffe der Algebraischen Zahlentheorie einführen um die Klassengruppe eines Zahlkörpers definieren zu können. Den Beweis, dass es sich hierbei um eine endliche abelsche Gruppe handelt soll skizziert werden. Danach soll ein Überblick gegeben werden, wie man die Klassengruppe nun algorithmisch berechnen kann.
- Definition aller notwendigen Konzepte damit die Klassengruppe eines Zahlkörpers definiert werden kann. (jedes Lehrbuch der Algebraischen Zahlentheorie e.g. (Neukirch 1992), (Cohen 2007) oder auch (Pohst 1993) und (Cohen 1993))
- Rest von Kapitel VII.1 in (Pohst 1993) insbesondere Minkowskischranke.
- Überblick über eine Methode zur Berechnung der Klassengruppe (Kapitel VII.2 in (Pohst 1993)).
Nach Bedarf und Interesse können wir dann noch untersuchen, wie man die gelernten Algorithmen unter bestimmten Bedingungen verbessern kann, beispielsweise gibt es schnellere Algorithmen für Quadratische Zahlkörper. Man könnte sich aber auch Beispiele für Kryptographieverfahren ansehen, die auf diesen Problemstellungen basieren oder versuchen zu verstehen, warum Quantencomputer einen beträchtlichen speed-up bringen werden.
Termine
Es wird eine Vorbesprechung zum Seminar am 11. April um 14 Uhr im Raum B 448 (Sozialraum im 4. Stock) bei der wir die Themenverteilung machen wollen.
Das Seminar ist für Donnerstag Nachmittag 12:30-14:00. Raum B133.
Anmeldung
Falls Sie an diesem Seminar teilnehmen wollen, senden Sie mir bitte so schnell wie möglich eine E-Mail an hofer@math.lmu.de. Die Teilnehmerzahl ist auf 8 Studierende begrenzt.
Literatur
Cohen, Henri. 1993. A course in computational algebraic number theory. Vol. 138. Graduate Texts in Mathematics. Springer-Verlag, Berlin.
----. 2007. Number theory. Vol. I. Tools and Diophantine equations. Vol. 239. Graduate Texts in Mathematics. Springer, New York.
Neukirch, Jürgen. 1992. Algebraische Zahlentheorie. Springer-Verlag, Berlin.
Pohst, Michael E. 1993. Computational algebraic number theory. Vol. 21. DMV Seminar. Birkhäuser Verlag, Basel.
Pohst, M., and H. Zassenhaus. 1989. Algorithmic algebraic number theory. Vol. 30. Encyclopedia of Mathematics and its Applications. Cambridge University Press, Cambridge.
Tatsächlich sind der Ganzheitsring von \(\mathbb{Q}\) die ganzen Zahlen \(\mathbb{Z}\). back
mit einer angepassten Komplexitätsdefinition back
"ohne Beweis" heißt für uns, dass Sie den Beweis nicht präsentieren sollen, in der Vorbereitung soll dieser aber schon studiert werden. back
Der Beweis dieser Aussage wird nächstes Semester in der Algebraischen Zahlentheorie nachgeliefert. back
Achtung, hier ist nicht eine Ordnungsrelation gemeint. back
Der Beweis wird in der Algebraischen Zahlentheorie nachgeliefert. back

