Where to go from here?¶
The step from the Perceptron to Adaline mainly brings two advantages:
- We may make use of analytic optimization theory;
- We may encode what we mean by ‘optimal’ weights
, i.e., by the terms ‘accurately’ and ‘generalizes’ of the introductory discussion, by the choice of the corresponding loss function.
This freedom leads to a rich class of linear classifiers, parametrized by the
choice of activation function and the form of loss function
. As there is great freedom in this choice we must understood
better how we can encode certain learning objectives in this choice. We shall
look in more detail at two different choice from (11) and
(12) in the next chapters. One of them results in the
industry-proven ‘support vector machine’ (SVM) model.
Discuss how the ‘optimal’ choice of weights is influence by changing the loss function (12) to
where
is the usual
-norm for
.
Give an example of a loss function employing a notion of distance other than the Euclidean one and implement the corresponding Adaline.
Sigmoid activation function¶
One of the widely employed choices in machine learning models that are based on
the Adaline framework are sigmoid functions. This class of functions is usually
defined as bouded differentiable function with a
non-negative derivative. Two frequent examples are the logistic function
(18)¶
and the hyperbolic tangent
Compared to the linear activation in (11) these functions often have several advantages.
First, their ranges are bounded by definition. In the cases considered above,
in which there are only two class labels, say or or
, the linear activation function (11) may attain
values much lower or higher that the numbers used to encode the class labels.
This may lead to extreme updates according to the update rule
(16) as the difference
may become very large. In the Adaline case considered above in which
we only had one output signal we did not encounter problems during training
because of such potentially large signals. On the contrary they were rather
welcome as they pushed the weight vector strongly in the right direction.
However, soon we will discuss the Adaline for multiple output signals
representing a whole layer of neurons, and furthermore, stack them on top of
each other to form multiple-layer networks of neurons. In these situation such
extreme updates will be undesired and the sigmoid function will work to prevent
them. Note that if we then replace the linear activation by the hyperbolic
tangent above, we ensure
, i.e., the updates are uniformly bounded as it was the case for the
Perceptron.
Second, the reason to consider multi-layer networks is to treat general non-linear classification problems and the necessary non-linearity will enter into the model by means of such non-linear activation functions.
Although both reasons are more important for the multi-layer networks considered later, it will be convenient to discuss the training of sigmoidal Adaline already for the simply case of only one output signal. Furthermore, there is a third reason why, e.g., the logistic is often preferred over the linear activation as the former can be interpreted as a probability.
The implementation of a sigmoidal Adaline is straight forward. We replace the
activation function accordingly, compute its derivative and adapt
the update rule (16).
Adapt our Adaline implemetation to employ
- the hyperbolic tangent activation function and
- the logistic function
and observe the corresponding learning behavior.
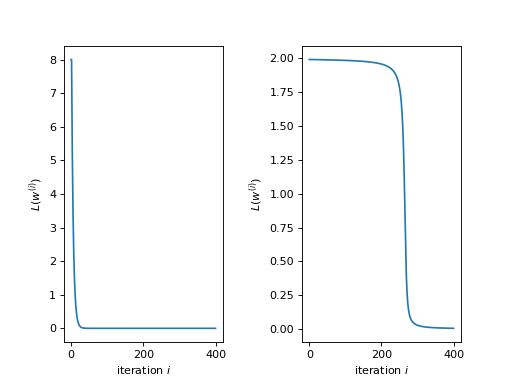
The implementation for the Iris data set should work out of the box having initial weight set to zero. However, one may recognize that the training for extreme choices of initial weights will require many epochs of training in order to achieve a reasonable accuracy. The following plots illustrate the learning behavior of a linear and hyperbolic tangent Adaline:
Both plots show the quadratic loss functions (12) per iteration of
training of a linear (left) and a hyperbolic tangent (right) Adaline. Both
started with an initial weight of and were presented the signle
training data element
. The initial weight
was chosen far off a reasonable value. Nevertheless, the linear Adaline
learns to adjust the weight rather quickly while the hyperbolic tangent
Adaline takes about more than two magnitudes more iteration before a
significant learning progress can be observed.
For simplicity and to draw a nice connection to statistics, let us look
at the logistic Adaline model, i.e., the Adaline model with
being the logistic function (18). The same line of reasoning that
will be developed for the logistic Adaline will apply to the hyperbolic tangent
Adaline in the plot above.
Looking at our update rule (16) we can read off the explanation for the slow learning phenomenon. Recall the update rule:
and the derivative of the logistic function (18):
(19)¶
Clearly, for large values of the derivative
becomes very small, and hence, the update computed by the update rule
(16) will be accordingly small even for the case of a
misclassification. This is why this phenomenon is usually referred to as
vanishig gradient problem.
If, for whatever reason, we would like to stick with the logistic function as
activation function we can only try to adapt the loss function in
order to better the situation. How can this be done? Let us restrict our
consideration to loss functions of the form
(20)¶
note that with
(21)¶
the form (20) reproduces exactly the form of the quadratic loss function given in (12). We compute
(22)¶
This means that the only choice to compensate a potential vanishing gradient
due to is to choose a good function
. Bluntly, this
could be done by choosing
to be proportional to the inverse of
and then integrating it – hoping to find a
useful loss function for the training objective. We will not follow this route
this but make a detour and use this opportunity to motivate a good candidate of
the loss function by ideas drawn from statistics. The direct way, however,
makes up a good homework and stands for its own as it is independent of the
heuristics.
For this purpose we introduce the concept of entropy and cross-entropy. We define:
Definition (Entropy) Given a discreet probability space
we define the so-called entropy by
Note that but the sum is to be understood as summing
only over
such that
. when excluding events
of probability zero as they since they would not have to to be encoded anyway.
Heuristically speaking, the entropy function
measures how many
bits are on average necessary to encode an event. Say Alice and Bob want to
distinguish a number of
events but only have a communication
channel through which one bit per communication can be send. An encoding scheme
that is able distinguish
events but on average minimizes the number
of communications between Alice and Bob would allocate small bit sequences for
frequent events and longer ones for infrequent ones. The frequency of an event
is is determined by
so that the best
strategy to minimize the average number of bits per event is to to allocate for
event
a number of
bits.
Let us regard a three examples:
A fair coin: The corresponding probability space can be modelled by
so that we find
Hence, on average we need 1 bit to store the events as typically we have 0 or 1.
A fair six-sided dice: The corresponding probability space can be modelled by
and we find
Hence, on average we need 3 bits to store which of the six typical events occurred.
An unfair six-sided dice: Let us take again
but instead of the uniform distribution like above we chose:
In this case we find
Since typically event
occurs more often then the others we may afford to allocate less bits to represent it. The price to pay is to allocate more bits for the less frequent events. However, weighting with the relative frequency, i.e., on average, such an allocation turns out to require less bits per event to be transmitted through Alice and Bob’s communication channel. In particular, on average, they need less bits than in the case of the fair dice.
In statistics the actual probability measure is usually unknown and the
objective is to find a good estimate
of it taking in account the empirical
evidence. A candidate for a measure of how good such a guess is is given by the
so-called cross-entropy which we define now.
Definition (Entropy) Given a discreet probability space
and another measure
we define the so-called
cross-entropy by
One may interpret as follows: If
is an estimate of the
actual probability measure then
is the number of bits
necessary to encode the event
according to this estimate. The
cross-entropy
is therefore an average w.r.t. to the actual
measure
of the number of bits needed to encode the events
according to
. If according to
we
would allocate the wrong amount of bits to encode the events Alice and Bob
would on average have to exchange more bits per communication. This indicates
that
must be the optimum which is actual:
Theorem (Cross-Entropy) Let be a discreet
probability space and
another measure on
. Then we
have:
This property qualifies as a kind of distance between a
potential guess
of the true probability
. After this
excursion to statistics let us employ this distance and with it build a loss
function for the logistic Adaline by the following analogy.
For the logistic Adaline we assume the labels for features to be
of the form
,
. Furthermore, we
observe that by definition also the activation functions evaluate to
. This allows to define for the sample space
and the following probability distributions, i.e., the actual one (assuming the
training data was labeled correctly and the are drawn with a
uniform distribution),
and the neuron’s guess (which for sake of the probabilistic analogy we interpret as a probability),
In order to measure the discrepancy between the actual measure
and the guess
we employ the cross-entropy, which in our
case, is defined as
Dropping the irrelevant constants we may define a new loss function
by using the following expression for (20)
(23)¶
so that we get
Using (19) we compute the derivative
We observe, that the vanishing gradient behavior of is
compensated by the derivative of the cross-entropy
. In conclusion,
we find the update rule corresponding to this new loss function
A comparison with the previous update rule (22) shows that
with the help of a change of loss function we end up with a update rule that
will not show the vanishing gradient problem. As a rule of thumb one can expect
that logistic Adalines will almost always be easier to train with cross entropy
loss functions unless the vanishing gradient effect is desired – at a
later point we may come back to this point and discuss that, e.g., in
convolution networks the ReLu activation function (being zero for negative
arguments and linear for positive ones) have actually proven to be very
convenient. For now the take away from this section is that the choices in
and
must be carefully tuned w.r.t. each other.
Support Vector Machine¶
While the Adaline loss functions (20) for the quadratic loss
(21) or cross-entropy loss (23) were good
measures of how accurately the training data is classified that can be used for
optimization in terms of gradient descent, they did not put a particular
emphasis on how the optimal weights may lead to a good generalization
from the classification of “seen” training data to “unseen” data we may want to
classify in the future. In the next model we shall specify such a sense and
derive a corresponding loss function.
Hard Margin Case¶
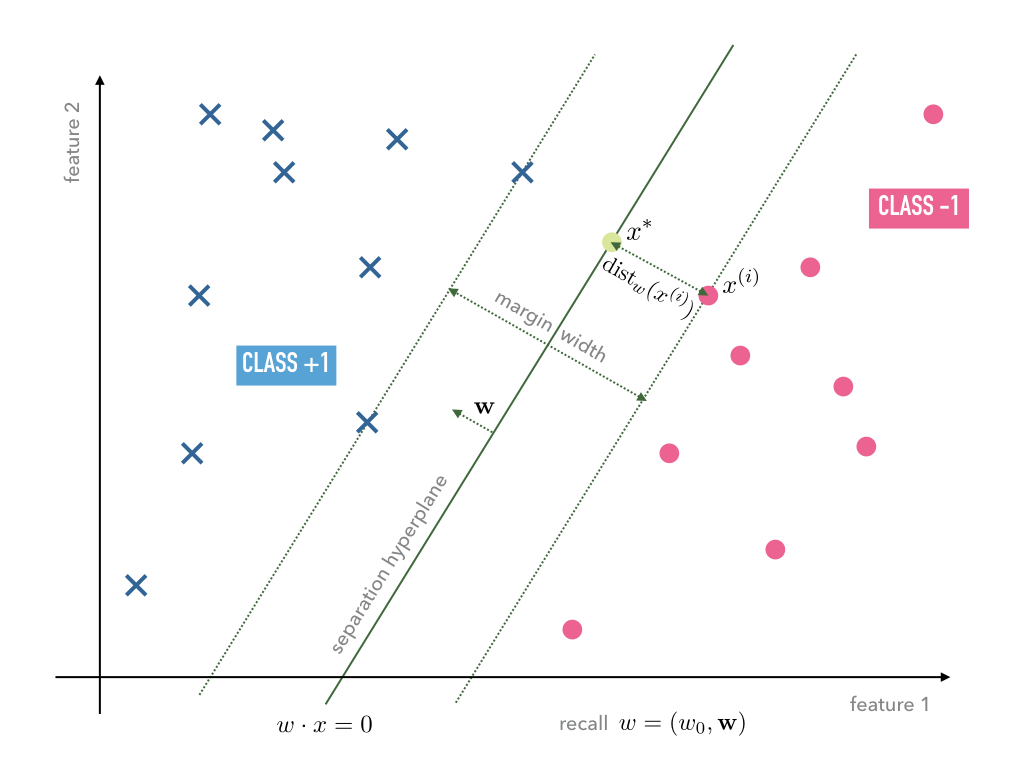
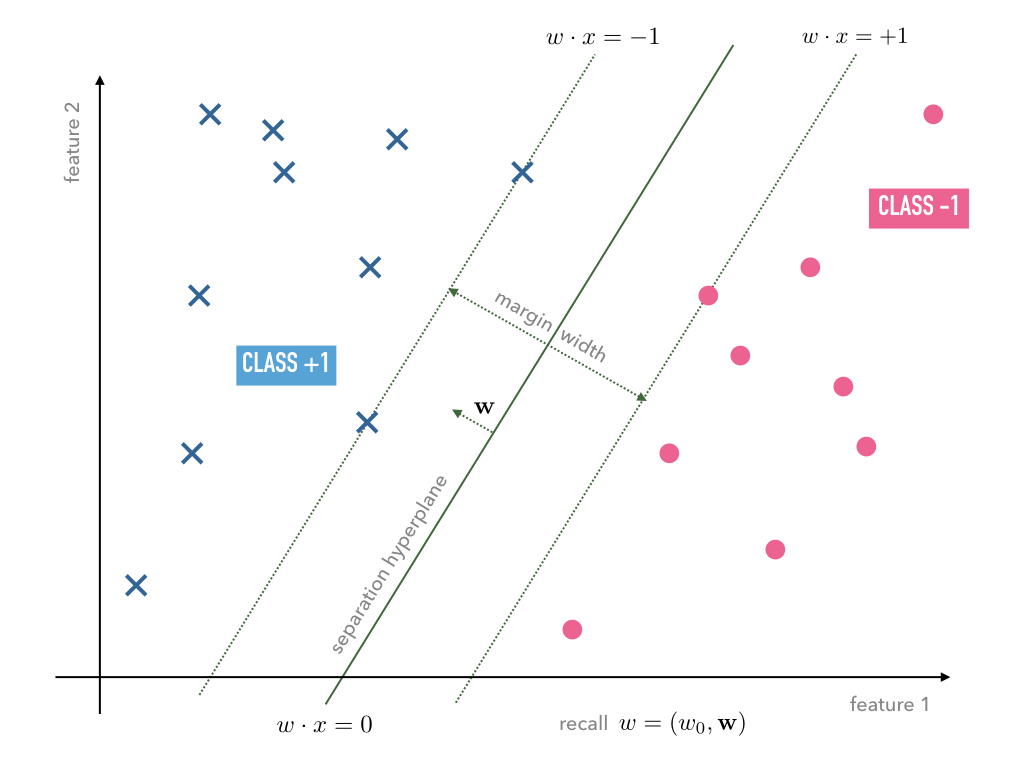
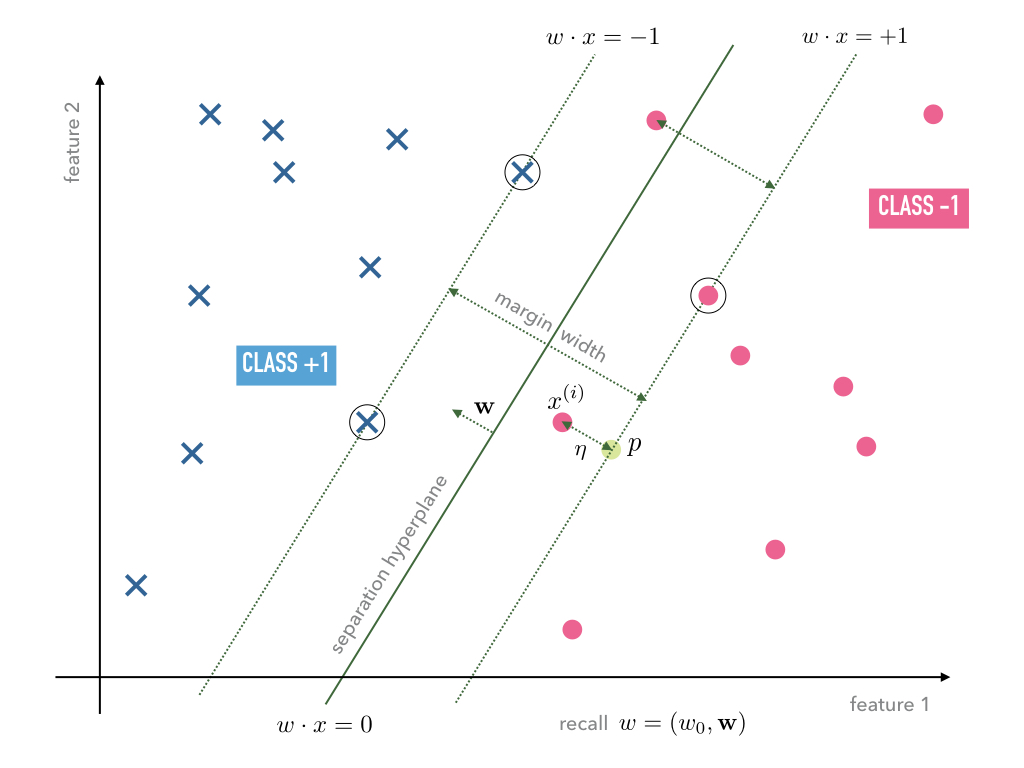
Consider a typical linear separable case of training data. Depending on the initial weights both, the Adaline and Perceptron, may find separating hyperplanes of the same training data, however, the hyperplanes are usually not unique. Among all possible hyperplanes it may make sense to choose the one that maximizes the margin width as, e.g., shown in Figure Fig. 6.
In order to set up an optimization program that maximizes the margin width, let
us compute the distance between a data point and the hyperplane
. For this purpose we
exploit that the vector
is the normal vector on the plane.
Hence, the straight line in direction of the normal vector
through the point
may be parametrized as follows
(24)¶
Recall again that the first coefficient in the vector
was chosen to remain equal one by our convention. Furthermore, by definition,
all points
on the hyperplane
fulfill
Hence, we have to solve the equation
for in order to compute the intersection point
between the straight line (24) and the hyperplane
:
The distance can then be computed by taking the difference
which results in
Any optimization program should, hence, choose a hyperplane that
classifies the data points correctly according to their labels
while trying to maximize the distance
for such
whose corresponding data points
lie within
minimal distance to the hyperplane – such points will in the following be
called support vectors, hence, the name support vector machine. In order
to make this notion precise without complicating the equations, we may exploit
the scale invariance of the hyperplane equation
which may be
build into the norm of
and simply define the minimal distance between
the nearest data points
to the hyperplane
equal to
one so that all other distances are measured in this unit.
On that scale, support vectors fulfill
so that
Using this, we can formulate the constraints as we must require that the
distance of any data point to the respective hyperplane
is larger or equal one. Hence, we may formulate
the optimization program as
If we prefer, this program is equivalent to
(25)¶
Note that the type of optimization is different to the one we have employed for the Adaline since now we need obey certain constraints during the optimization. Before we get to an implementation let us regard a useful generalization of this so-called hard margin case in which we do not allow any violation of the margin width.
Soft Margin Case¶
The optimization program (25) is very dependent on the
fluctuation of data points near the margin. Possible outliers in the training
data near or within the margin dictate how the “optimal” weights have
to be chosen. To reduce this dependency we shall extend the hard margin program
to the so-called soft-margin program as follows.
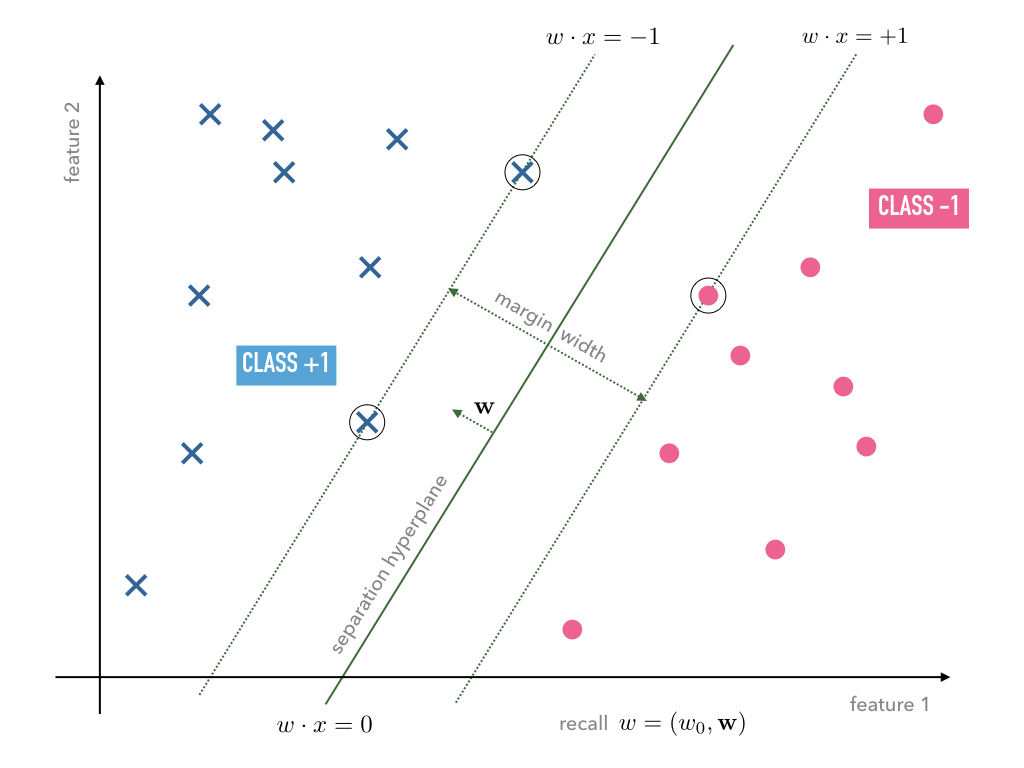
Let us in general allow margin violations but include in the optimization
program that those have to be minimized. Suppose violates the
margin width. This means that either
in which case it is only a margin violation but not a misclassification or
in which case it is a margin violation that leads to a misclassification,
which are illustrated in the following Figure Fig. 9
The depth of a potential margin violation of data point can be
computed following the same strategy as above. First, we compute the orthogonal
projection
of
onto the hyperplane
as depicted in Figure Fig. 9, i.e., the point
is given by the intersection of the straight line
and the hyperplane
since the label determined the sign on the right-hand side.
Hence, we have to solve the equation
for which gives
The depth of the margin violation is then given by the distance
In order to allow for margin violations but also minimize them, we may now set up the following optimization program
If we now change the scale once more to units of the
program can be stated equivalently as
(26)¶
Implementation¶
In order to arrive at our first, as it will turn out, naive, implementation of the support vector machine for the soft margin case, we need to implement a version of the optimization program (26) and we shall do so in the spirit of the Adaline model. Later we will see that this can be done much more elegantly by reformulating the optimization program.
For this purpose we need a loss function to mimic the behavior of the program (26). A good candidate for this is given by
(27)¶
where denotes the maximum of a set
,
is a
parameter that controls the weight with respect to which the minimization of
is prioritized over the minimization of the
accumulative margin violation. The factor
is just decoration,
of course, and only kept because you will see it in many textbooks.
We may now be tempted to readily apply a gradient descent algorithm in order to
find optimal weights . However, we recall that for this we need
to be a differentiable function of
and due to the
function this is not the case. Nevertheless, we can approximate
the derivative by means of a suitable candidate of its subdifferential. For
example, we may simple set approximate gradient to be
(28)¶
and use the update rule
for some learning parameter . To render the
implementation of the update rule more transparent let us first create a class
of methods that performs the computation of the loss function (27)
as well as the approximate gradient (28):
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 | class LossSVM:
def __init__(self, X_train, Y_train, mu=1.0):
"""
Initialize the parameter `mu` which specifies the weighting
between margin width and the distance to the support vectors, and
furthermore, the training data `X_train` and `Y_train`.
"""
self.mu_ = mu
self.xi_ = X_train
self.yi_ = Y_train
return
def val(self, w):
"""
Computes a value of the loss function for a given weight vector.
"""
self.margin = 1 - self.yi_ * ( np.dot(self.xi_, w[1:]) + w[0] )
w_norm = 1/2 * np.sum( w[1:]**2 )
margin_violations = np.where(self.margin >= 0, self.margin, 0)
margin_avg = margin_violations.sum() / len(self.xi_)
return w_norm + self.mu_ * margin_avg
def diff(self, w):
"""
Computes the derivative of the loss function for a given weight vector.
"""
self.margin = 1 - self.yi_ * ( np.dot(self.xi_, w[1:]) + w[0] )
w0_sub_diff1 = - self.yi_
w0_sub_diffs = np.where(self.margin >= 0, w0_sub_diff1, 0)
w0_diffs_avg = w0_sub_diffs.sum() / len(self.xi_)
w_sub_diff1 = - self.xi_ * self.yi_[:,np.newaxis]
w_sub_diffs = np.where(self.margin[:,np.newaxis] >= 0, w_sub_diff1, 0)
w_diffs_avg = w_sub_diffs.sum(axis=0) / len(self.xi_)
ret0 = np.array([ w0_diffs_avg ])
ret_vec = w[1:] + self.mu_ * w_diffs_avg
return np.append(ret0, ret_vec)
|
- This class expects the training data as arguments
X_trainandY_trainin the constructor in line 3; - The
val()method in line 15 determines the value of the loss function for the training data specified in the constructor; - Furthermore, the method
diff()computes the approximate derivative stated in (28).
The rest of the implementation follows the Adline one except, of course, that the learning rule has to be replaced:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 | def learn(self, X_train, Y_train, mu=1.0, eta=0.01, epochs=1000):
'''
fit training data according to eta and n_iter
and log the errors in errors_
'''
# we initialize two list, each for the misclassifications and the cost function
self.train_errors_ = []
self.train_loss_ = []
# for all the epoch
for _ in range(epochs):
# classify the traning features
Z = self.classify(X_train)
# count the misqualifications for the logging
err = 0
for z, y in zip(Z, Y_train):
err += int(z != y)
# ans save them in the list for later use
self.train_errors_.append(err)
loss = LossSVM(X_train, Y_train, mu=mu)
# compute loss for this epoch
self.train_loss_.append( loss.val(self.w_) )
# compute gradient of loss function and with it the update for w
delta_w = - eta * loss.diff(self.w_)
# update the weights
self.w_ += delta_w
return
|
- The
LossSVMclass that we defined above is instantiated withlossin the main loop and the entire training data is passed to its constructor; - The computation of the loss function is carried out in line 24 while the update happens in line 26.
SOURCECODE: where_to_go/iris_svm.ipynb
The full implementation of the ‘naive’ version of the support vector machine.
SOURCECODE: where_to_go/iris_svm_convergence.ipynb
These are the same test scenarios that we used to observe the learning behavior for the Perceptron and Adaline.
mu and eta in scenarios that feature
margin violations in order to get a feeling about their influence.