Arbeitsfeld




Next: Auswahl aktueller Veröffentlichungen
Up: Prof. Dr. Wilfried Buchholz
Previous: Prof. Dr. Wilfried Buchholz
Mein Arbeitsgebiet ist die Beweistheorie, ein Teilgebiet der Mathematischen
Logik, in dem formale Beweise und Transformationen an formalen
Beweisen untersucht werden.
Die Beweistheorie ist vor ca. 70 Jahren von David Hilbert begründet
worden, um in ihr die Widerspruchsfreiheit der klassische Mathematik
(bzw. wesentlicher Teile davon) mit streng finiten Mitteln nachzuweisen (Hilbertsches Programm).
Die Untersuchungen von Gödel haben jedoch bald darauf gezeigt, daß das
Hilbertsche Programm (in seiner ursprünglich Form) nicht durchzuführen ist.
Daraus ergab sich zwangsläufig eine Verschiebung der beweistheoretischen Zielsetzung.
Ein Hauptanliegen der heutigen Forschungen in der Beweistheorie (und meiner
eigenen Arbeit, siehe z.B. [3],[4] und die Bücher [2],[3]) ist die
genaue Charakterisierung der Beweisstärke von mathematisch relevanten Axiomensystemen.
Ein wichtiges Hilfsmittel dabei sind gewisse konkrete Repräsentationen von Wohlordnungen
(sog. Bezeichnungssysteme für Ordinalzahlen).
Man charakterisiert die Beweisstärke eines Axiomensystems 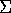 z.B. durch
das Supremum aller Ordungstypen von Ordinalzahlbezeichnungssystemen, für die
die Wohlordnungseigenschaft in
z.B. durch
das Supremum aller Ordungstypen von Ordinalzahlbezeichnungssystemen, für die
die Wohlordnungseigenschaft in 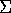 beweisbar ist.
Die Kenntnis dieser ``beweistheoretische Ordinalzahl''
beweisbar ist.
Die Kenntnis dieser ``beweistheoretische Ordinalzahl'' 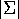 liefert
in der Regel eine
Fülle von Informationen über die Menge der in
liefert
in der Regel eine
Fülle von Informationen über die Menge der in 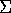 beweisbaren Sätze.
Davon abgesehen ist
beweisbaren Sätze.
Davon abgesehen ist 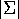 aber auch unter dem ursprünglichen Aspekt des Hilbertschen Programms von Interesse,
denn in den meisten Fällen ist
aber auch unter dem ursprünglichen Aspekt des Hilbertschen Programms von Interesse,
denn in den meisten Fällen ist 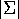 gerade gleich der kleinsten Ordinalzahl
gerade gleich der kleinsten Ordinalzahl 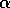 derart,
daß aus dem Prinzip der transfiniten Induktion bis
derart,
daß aus dem Prinzip der transfiniten Induktion bis 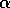 die Widerspruchsfreiheit
von
die Widerspruchsfreiheit
von 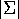 in finiter Weise gefolgert werden kann.
in finiter Weise gefolgert werden kann.
Methoden und Resultate der Beweistheorie sind auch für einige Bereiche der theoretischen Informatik
von Bedeutung.
So spielen z.B. Ordinalzahlbezeichnungssysteme und (konstruktive) Wohlordnungsbeweise
eine wichtige Rolle bei der Behandlung von Terminierungs- und Komplexitätsfragen für
Termersetzungssysteme.
In [5] konnte ich durch die Analyse von Wohlordnungsbeweisen
einen interessanten Zusammenhang zwischen dem Ordnungstyp einer
Terminierungsordnung 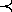 und der maximalen Länge von
Reduktionsfolgen eines unter
und der maximalen Länge von
Reduktionsfolgen eines unter 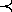 reduzierenden Termersetzungssystems
herstellen.
Ein anderes Thema der Beweistheorie,
mit dem ich mich seit langem beschäftige (vergl. Bücher
[2]), und das seit einiger Zeit auf verstärktes Interesse
in der theoretischen Informatik stößt, ist die Analyse von Theorien induktiver Definitionen
und damit verwandter sog. Fixpunkt-Theorien (vgl. [7]).
reduzierenden Termersetzungssystems
herstellen.
Ein anderes Thema der Beweistheorie,
mit dem ich mich seit langem beschäftige (vergl. Bücher
[2]), und das seit einiger Zeit auf verstärktes Interesse
in der theoretischen Informatik stößt, ist die Analyse von Theorien induktiver Definitionen
und damit verwandter sog. Fixpunkt-Theorien (vgl. [7]).
Hauber
Wed Nov 20 16:14:16 MET 1996
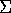 z.B. durch
das Supremum aller Ordungstypen von Ordinalzahlbezeichnungssystemen, für die
die Wohlordnungseigenschaft in
z.B. durch
das Supremum aller Ordungstypen von Ordinalzahlbezeichnungssystemen, für die
die Wohlordnungseigenschaft in 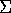 beweisbar ist.
Die Kenntnis dieser ``beweistheoretische Ordinalzahl''
beweisbar ist.
Die Kenntnis dieser ``beweistheoretische Ordinalzahl'' 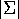 liefert
in der Regel eine
Fülle von Informationen über die Menge der in
liefert
in der Regel eine
Fülle von Informationen über die Menge der in 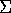 beweisbaren Sätze.
Davon abgesehen ist
beweisbaren Sätze.
Davon abgesehen ist 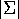 aber auch unter dem ursprünglichen Aspekt des Hilbertschen Programms von Interesse,
denn in den meisten Fällen ist
aber auch unter dem ursprünglichen Aspekt des Hilbertschen Programms von Interesse,
denn in den meisten Fällen ist 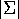 gerade gleich der kleinsten Ordinalzahl
gerade gleich der kleinsten Ordinalzahl 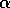 derart,
daß aus dem Prinzip der transfiniten Induktion bis
derart,
daß aus dem Prinzip der transfiniten Induktion bis 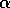 die Widerspruchsfreiheit
von
die Widerspruchsfreiheit
von 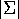 in finiter Weise gefolgert werden kann.
in finiter Weise gefolgert werden kann.
 und der maximalen Länge von
Reduktionsfolgen eines unter
und der maximalen Länge von
Reduktionsfolgen eines unter