Forschungsgebiete

1. Funktionalanalysis
   Hauptgegenstand in Forschung und Lehre sind hier die Theorie (nicht-) linearer Operatoren in allgemeinen und in speziellen Banachräumen (z.B. auf Räumen stetiger Funktionen), vektorwertige Maße, Geometrie der Banachräume, topologische Vektorräume, Charakterisierungen spezieller Mengen in klassischen Banachräumen (z.B. der schwach kompakten). Die Theorie der 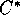-Algebren und der Nichtkommutativen Integration wird besonders von dem am Lehrstuhl tätigen Priv.-Doz. Dr. G. Schlüchtermann vertreten.
   
2. Gewöhnliche und Partielle Differentialgleichungen
   Der Schwerpunkt in Forschung und Lehre liegt hier auf den Differentialgleichungen der Mathematischen Physik, insbesondere der Transporttheorie, wie sie in der Theorie verdünnter Gase mit der Boltzmann-Gleichung und in der Stellardynamik und der Plasmaphysik im Vlasov-Poisson-System und dem Vlasov-Maxwell-System und in einer Vielzahl verwandter Systeme partieller Diferentialgleichungen auftreten. Diese Systeme bestehen in der Regel aus einer Differentialgleichung erster Ordnung und aus elliptischen, bzw. hyperbolischen Gleichungen zweiter Ordnung in nichtlinearer Verkoppelung. Das Anfangswertproblem der Stellardynamik ist seit 1952 als solches bekannt, konnte aber nach umfangreichen Vorarbeiten auf internationaler Ebene erst 1989 in München klassisch global in befriedigender Weise gelöst werden. Das Anfangswertproblem der Plasmaphysik ist allgemein klassisch global noch offen, trotz entscheidender Fortschritte durch R. Glassey und W. Strauss (USA) und P.L. Lions (Frankreich). Andere Probleme sind die Existenz stationärer oder räumlich periodischer Lösungen (hier finden Methoden der Nichtlinearen Funktionalanalysis Anwendung), expliziter Lösungen, Fragen der Stabilität und der Asymptotik für 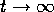. An der Lösung dieser Fragen sind Astrophysiker und Plasmaphysiker in gleicher Weise interessiert. Die physikalische Literatur ist voller Ansätze zu diesen Fragen, die vielfach aber mathematischer Nachprüfung nicht standhalten. Dieses gilt in hohem Maß für die dort gemachten Angaben über die Stabilität, so daß ein weites Feld mathematischer Forschung eröffnet wird. - Der am Lehrstuhl tätige Priv.-Doz. Dr. G. Rein hat kürzlich in seiner Habilitationsschrift und in Vorarbeiten mit der Untersuchung der mit der Vlasov-Gleichung gekoppelten Einsteinschen Feldgleichungen ein neues Arbeitsgebiet in die am Lehrstuhl verfolgten Fragestellungen eingebracht.