Arbeitsfeld




Next: Auswahl aktueller Veröffentlichungen
Up: Prof. Dr. Wolfgang Zimmermann
Previous: Prof. Dr. Wolfgang Zimmermann
Mein Arbeitsgebiet ist die Strukturtheorie von Ringen und Moduln. In den zurückliegenden
Jahren bewegte sich meine Forschungstätigkeit vorwiegend in zwei Teilgebieten, die sich
zunehmend gegenseitig anregten und durchdrangen.
Die genaue Kenntnis der algebraisch kompakten Moduln über einen Ring ist deshalb von
Bedeutung, weil jeder andere Modul reiner Untermodul eines solchen ist. Algebraisch kompakte
Moduln sind im wesentlichen ,,duale Moduln``, sie besitzen gute Struktureigenschaften und
können in sehr unterschiedlicher Weise gekennzeichnet werden (algebraisch, topologisch,
homologisch, modell-theoretisch). Eine der subtilsten Beschreibungen, die auch zu einer genauen
internen Charakterisierung 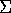 -algebraisch kompakter Moduln führte,
verwendet sogenannte matrizielle Untergruppen [5].
Es hat sich mittlerweile herausgestellt, daß diese ein äußerst nützliches
Hilfsmittel der Modultheorie sind.
Beispielsweise konnte mit ihrer Hilfe eine Teilantwort zu
einem berühmten Problem der Darstellungstheorie bewiesen werden [7].
Derzeit arbeite ich am weiteren Ausbau der ,,matriziellen Modultheorie``,
in erster Linie untersuche ich Moduln mit
Kettenbedingungen für matrizielle Untergruppen [8].
-algebraisch kompakter Moduln führte,
verwendet sogenannte matrizielle Untergruppen [5].
Es hat sich mittlerweile herausgestellt, daß diese ein äußerst nützliches
Hilfsmittel der Modultheorie sind.
Beispielsweise konnte mit ihrer Hilfe eine Teilantwort zu
einem berühmten Problem der Darstellungstheorie bewiesen werden [7].
Derzeit arbeite ich am weiteren Ausbau der ,,matriziellen Modultheorie``,
in erster Linie untersuche ich Moduln mit
Kettenbedingungen für matrizielle Untergruppen [8].
Ihr Ziel ist es, die Modulkategorie zu einem ,,konkret`` gegebenen artinschen Ring möglichst
genau zu beschreiben. Ein erster wichtiger Schritt ist die Auflistung und Beschreibung der
endlich erzeugten unzerlegbaren Moduln sowie der Homomorphismen dazwischen. Zu diesem
Problem wurden in den vergangenen 25 Jahren mit völlig neuen Methoden außerordentlich
eindrucksvolle Ergebnisse erzielt. Einen zentralen Platz unter diesen neuen Instrumentarien
nimmt die Theorie der Auslander-Reiten-Folgen ein. Die Existenz solcher Folgen war zuerst von
Auslander und Reiten für endlich erzeugte Moduln über Artin-Algebren bewiesen worden.
Dagegen gibt es zum Problem der Existenz über Artin-Ringen, die nicht Artin-Algebren sind,
viele offene Fragen: In diesem Fall brauchen Auslander-Reiten-Folgen nicht mehr zu existieren;
falls sie aber existieren, haben sie eventuell völlig andere Eigenschaften als im Algebren-Fall [6].
Zu diesem interessanten und schwierigen Gebiet konnten meine Doktoranden L. Angeleri Hügel
und M. Schmidmeier ausgezeichnete Resultate beitragen.
Hauber
Wed Nov 20 16:14:16 MET 1996
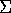 -algebraisch kompakter Moduln führte,
verwendet sogenannte matrizielle Untergruppen [5].
Es hat sich mittlerweile herausgestellt, daß diese ein äußerst nützliches
Hilfsmittel der Modultheorie sind.
Beispielsweise konnte mit ihrer Hilfe eine Teilantwort zu
einem berühmten Problem der Darstellungstheorie bewiesen werden [7].
Derzeit arbeite ich am weiteren Ausbau der ,,matriziellen Modultheorie``,
in erster Linie untersuche ich Moduln mit
Kettenbedingungen für matrizielle Untergruppen [8].
-algebraisch kompakter Moduln führte,
verwendet sogenannte matrizielle Untergruppen [5].
Es hat sich mittlerweile herausgestellt, daß diese ein äußerst nützliches
Hilfsmittel der Modultheorie sind.
Beispielsweise konnte mit ihrer Hilfe eine Teilantwort zu
einem berühmten Problem der Darstellungstheorie bewiesen werden [7].
Derzeit arbeite ich am weiteren Ausbau der ,,matriziellen Modultheorie``,
in erster Linie untersuche ich Moduln mit
Kettenbedingungen für matrizielle Untergruppen [8].